| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Интегральные оценки напряженного состояния
4.1. Моменты функции.
Условимся называть моменты  порядка функции
порядка функции  заданной в V-объеме, интегралы
заданной в V-объеме, интегралы

где  неотрицательные целые числа, сумма которых
неотрицательные целые числа, сумма которых

При  имеется
имеется  чисел
чисел  с суммой
с суммой  при
при  число чисел
число чисел  с суммой
с суммой  равно
равно  д. Поэтому общее число
д. Поэтому общее число  моментов
моментов  порядка равно
порядка равно

4.2. Моменты компонент тензора напряжений.
Уравнения равновесия в объеме (1.5.6) позволяют записать  соотношений
соотношений

Первое слагаемое преобразуется по формуле Гаусса — Остроградского

причем использованы уравнения равновесия на поверхности (1.5.15)

Теперь введя обозначения

придем к соотношениям

Их правые части при заданных объемных и поверхностных силах (по всей поверхности О, ограничивающей объем V) известны. Число уравнений (4.2.3) равно  , а число неизвестных — числу моментов
, а число неизвестных — числу моментов  порядка для шести функций
порядка для шести функций  то есть
то есть  .
.
4.3. Случаи n = 0, n = 1.
При  и три уравнения
и три уравнения

выражают условия обращения в нуль главного вектора внешних сил.
При  приходим к девяти уравнениям, содержащим шесть неизвестных; из них находим средние значения шести компонент тензора напряжений
приходим к девяти уравнениям, содержащим шесть неизвестных; из них находим средние значения шести компонент тензора напряжений

причем условия симметричности этого тензора

выражают требования обращения в нуль трех компонент  ного момента внешних сил.
ного момента внешних сил.
4.4. Моменты напряжений первого порядка.
При  приходим к 18 уравнениям с таким же числом неизвестных
приходим к 18 уравнениям с таким же числом неизвестных

Уравнения распадаются на две группы:

Из них находим все моменты первого порядка всех шести компонент тензора напряжений. Например, моменты первого порядка напряжений  (поделенные на объем) равны
(поделенные на объем) равны

4.5. Пример. Сосуд под внешним и внутреннимдавлением.
Объем тела обозначается  а внутренней полости
а внутренней полости  ограничивающие эти объемы поверхности назовем
ограничивающие эти объемы поверхности назовем  Поверхностные силы создаются равномерно распределенными по
Поверхностные силы создаются равномерно распределенными по  давлениями — внешним
давлениями — внешним  внутренним
внутренним  так что
так что

где  единичные векторы внешних по отношению к телу нормалей к поверхностям
единичные векторы внешних по отношению к телу нормалей к поверхностям  (вектор
(вектор  направлен внутрь полости
направлен внутрь полости  Начало системы осей совмещено с центром тяжести объема тела (материала), так что
Начало системы осей совмещено с центром тяжести объема тела (материала), так что

где  координаты центров тяжести объемов
координаты центров тяжести объемов 
По (4.2.1) при пренебрежении массовыми силами имеем

где  объем материала. Условия равновесия (4.3.1), (4.3.3), конечно, выполняются. По (4.3.2), (4.4.2), (4.4.3),
объем материала. Условия равновесия (4.3.1), (4.3.3), конечно, выполняются. По (4.3.2), (4.4.2), (4.4.3),
учитывая (4.5.2), находим средние значения нормальных напряжений и их первых моментов

Средние значения и первые моменты касательных напряжений равны нулю:

4.6. Пример. Главный вектор и главный момент напряжений в плоском сечении тела.
Рассматривается часть загруженного массовыми и поверхностными силами тела V, отсеченная от него плоскостью  Объем этой части назовем
Объем этой части назовем  он ограничен поверхностью
он ограничен поверхностью  где
где  — часть поверхности О тела
— часть поверхности О тела  площадь плоского сечения. При этих обозначениях, принимая
площадь плоского сечения. При этих обозначениях, принимая  в объеме
в объеме  имеем по (4.2.1)
имеем по (4.2.1)

так как  на плоскости
на плоскости  . В (4.6.1) первое слагаемое определяется заданными внешними силами. Из уравнений равновесия (4.3.1), (4.3.3) находим теперь выражения:
. В (4.6.1) первое слагаемое определяется заданными внешними силами. Из уравнений равновесия (4.3.1), (4.3.3) находим теперь выражения:
а) перерезывающих сил

б) растягивающей силы

в) крутящего момента

г) изгибающих моментов относительно осей 

Индексом  обозначается среднее значение по площади
обозначается среднее значение по площади 

4.7. Оценка среднего значения квадратичной формы компонент тензора напряжений.
Для упрощения записей здесь используются одноиндексные обозначения

В рассмотрение вводится положительная 6X6 матрица  постоянных. Через
постоянных. Через  обозначен интеграл по объему тела от знакоопределенной положительной квадратичной формы:
обозначен интеграл по объему тела от знакоопределенной положительной квадратичной формы:

(опущены знаки суммирований по  Система осей
Система осей  совмещена с главными центральными осями инерции объема
совмещена с главными центральными осями инерции объема

и вводятся обозначения

так что

представляют квадраты радиусов инерции относительно главных осей 
Рассматриваемая как функция коэффициентов  функция
функция  имеет минимум при условиях
имеет минимум при условиях

Поскольку определитель  из них следует, что стационарное значение
из них следует, что стационарное значение  являющееся вследствие ее знакоопределен ной положительности минимумом, достигается при значениях параметров
являющееся вследствие ее знакоопределен ной положительности минимумом, достигается при значениях параметров  равных
равных

и вычисляемых с помощью формул (4.3.2), (4.4.2), (4.4.3) по заданию внешних сил. Этот минимум, если еще раз обратиться к формулам (4.7.3), оказывается равным

Приходим к неравенству

Со знаком  оно имеет место и для положительной знакопостоянной формы
оно имеет место и для положительной знакопостоянной формы  Пусть, например, все
Пусть, например, все  кроме одного
кроме одного  равны нулю. Тогда
равны нулю. Тогда

В задаче о сосуде  по (4.5.3) и (4.5.4) неравенство
по (4.5.3) и (4.5.4) неравенство

согласно с (2.4.10) выполняется при  со знаком равенства. Пусть теперь
со знаком равенства. Пусть теперь  полагая только одно
полагая только одно  имеем неравенство
имеем неравенство

показывающее, что наличие полости сопровождается повышением напряжений; это следует из того, что при отсутствии полости  и по (2.4.10) в формуле (4.7.9) надо принять знак равенства.
и по (2.4.10) в формуле (4.7.9) надо принять знак равенства.
4.8. Оценка удельной потенциальной энергии деформированного линейно-упругого тела.
Эта величина, как будет показано в п. 3.2 гл. III, выражается через инварианты тензора напряжений по формуле

где  модуль Юнга,
модуль Юнга,  коэффициент Пуассона материала. Неравенство (4.7.6) позволяет дать следующую оценку этой величины; вычисляемую по заданию внешних сил. Обозначим
коэффициент Пуассона материала. Неравенство (4.7.6) позволяет дать следующую оценку этой величины; вычисляемую по заданию внешних сил. Обозначим

и также

(суммирование по индексу  от 1 до 3 с заменой
от 1 до 3 с заменой  единицей). Тогда
единицей). Тогда

4.9. Оценка удельной интенсивности касательных напряжений.
Квадрат этой величины, равный абсолютному значению второго инварианта девиатора тензора напряжения, по (2.2.11), а также со ссылкой на формулы (1.11.8), (1.10.5), может быть записан в виде

Это — знакопостоянная положительная форма, так как она обращается в нуль при  По (4.7.6) имеем
По (4.7.6) имеем

Согласно критерию Мизеса неравенство  во всем объеме тела
во всем объеме тела  предел текучести материала) гарантирует отсутствие в нем зон пластической деформации; поскольку
предел текучести материала) гарантирует отсутствие в нем зон пластической деформации; поскольку  то условие
то условие  представляет необходимое, но, конечно, не достаточное условие недостижимости предела текучести. Поэтому неравенство
представляет необходимое, но, конечно, не достаточное условие недостижимости предела текучести. Поэтому неравенство

является достаточным признаком наличия зон пластичности, тогда как неравенство противоположного знака

представляет необходимое условие их отсутствия. Как уже говорилось, эти критерии выражены с помощью формул  через внешние объемные и поверхностные внешние силы (последние предполагаются заданными по всей поверхности О тела).
через внешние объемные и поверхностные внешние силы (последние предполагаются заданными по всей поверхности О тела).
4.10. Моменты напряжений второго и более высокого порядка.
Если 3, то число уравнений (4.2.3) меньше числа неизвестных. Например, при  имеем 30 уравнений с 36 неизвестными. Однако 15 неизвестных (при любом
имеем 30 уравнений с 36 неизвестными. Однако 15 неизвестных (при любом  оказывается возможным определить. Это девять величин
оказывается возможным определить. Это девять величин

и шесть величин вида

4.11. Оценка снизу максимума компонент напряжений.
Вывод формулы (4.7.6) для оценки снизу среднего значения квадратичной формы компонент тензора напряжений основывался только на свойствах ортонормированности (4.7.3), (4.7.4) в объеме V четырех полиномов (нулевой и первой степени)

и его можно применить к более общей системе ортонормированных полиномов

Например, к основной системе (4.11.1) можно присоединить один из полиномов второй степени

причем

Вычисление становится более громоздким при присоединении к основной системе не одного, а двух полиномов, например полинома  и полинома
и полинома  содержащего
содержащего  тогда придется позаботиться об ортогональности
тогда придется позаботиться об ортогональности  не только с основными полиномами, но с
не только с основными полиномами, но с 
Пусть построена ортонормированная в V система полиномов

Тогда введя в рассмотрение вместо (4.7.2) выражение более общего вида

и повторив вывод в п. 4.7, придем к более общему, чем (4.7.6), неравенству

причем знак равенства может иметь место, если  знакопостоянная положительная форма.
знакопостоянная положительная форма.
Пусть все  кроме одного с одинаковыми индексами, равны нулю. Тогда, учитывая, что
кроме одного с одинаковыми индексами, равны нулю. Тогда, учитывая, что

придем к оценке снизу максимума модуля 

Она представляется весьма грубой, но ее можно уточнить, увеличивая ее правую часть путем присоединения новых ортонормированных в V полиномов. При выборе их, однако, надо позаботиться о возможности выразить величины

через вычисляемые по заданным нагрузкам моменты высоких порядков (4.10.1) и (4.10.2).
Например, если ограничиться в этих формулах  то при разыскании
то при разыскании  кроме основных полиномов (4.11.1), можно использовать еще построенный выше полином
кроме основных полиномов (4.11.1), можно использовать еще построенный выше полином  а для дальнейшего уточнения еще один полином, ортонормированный с предшествующими пятью полиномами, включающий слагаемое
а для дальнейшего уточнения еще один полином, ортонормированный с предшествующими пятью полиномами, включающий слагаемое  или
или  Дальнейшее уточнение требует уже построения системы семи ортонормированных полиномов (четырех основных и трех квадратичных, содержащих
Дальнейшее уточнение требует уже построения системы семи ортонормированных полиномов (четырех основных и трех квадратичных, содержащих  Этим при
Этим при  возможность дальнейшего уточнения
возможность дальнейшего уточнения  будет исчерпана. Аналогично строятся оценки максимумов остальных компонент. Например, наилучшая оценка при
будет исчерпана. Аналогично строятся оценки максимумов остальных компонент. Например, наилучшая оценка при  снизу
снизу  с помощью формулы (4.11.7) может быть достигнута с помощью шести полиномов: полиномов
с помощью формулы (4.11.7) может быть достигнута с помощью шести полиномов: полиномов  и ортонормированного с ними полинома, содержащего
и ортонормированного с ними полинома, содержащего 
4.12. Уточненная оценка.
Исходим из равенства

в котором  некоторые постоянные. Тогда, поскольку модуль интеграла в левой части не превосходит интеграла от модуля подынтегральной функции, имеем
некоторые постоянные. Тогда, поскольку модуль интеграла в левой части не превосходит интеграла от модуля подынтегральной функции, имеем

и, возвращаясь к (4.12.1), приходим к неравенству

Вхождение в знаменатель правой части интеграла от модуля существенно усложняет вычисление, но преимуществом этой
формулы по сравнению с (4.11.6) является наличие постоянных  распоряжаясь которыми можно увеличивать правую часть неравенства.
распоряжаясь которыми можно увеличивать правую часть неравенства.
Полагая

имеем по (4.11.6)

Теперь примем в неравенстве (4.12.2)

и через у назовем его правую часть:

Полагая  в известном неравенстве Буняковского — Шварца
в известном неравенстве Буняковского — Шварца

имеем

В приложении к знаменателю правой части (4.12.5) это неравен ство с учетом (4.11.5) дает

откуда следует, что

Итак, оценка снизу по неравенству (4.12.3) хуже, чем даваемая неравенством (4.12.2), если в последнем выбрать постоянные  по (4.12.4). Например, если только одна из постоянных отлична от нуля, то по (4.12.2) и (4.12.4)
по (4.12.4). Например, если только одна из постоянных отлична от нуля, то по (4.12.2) и (4.12.4)

и эта оценка точнее, чем (4.11.7).
В качестве примера приведем оценку снизу максимума модуля температуры 0 линейно-упругого тела при адиабатическом нагружении. По (3.5.8) гл. III имеем

где  — температура, отсчитываемая от натурального состояния (при отсутствии нагружения),
— температура, отсчитываемая от натурального состояния (при отсутствии нагружения),  абсолютная температура в этом состоянии, а — коэффициент линейного расширения,
абсолютная температура в этом состоянии, а — коэффициент линейного расширения,  теплоемкость при постоянном давлении; через а обозначен первый вариант тензора напряжения
теплоемкость при постоянном давлении; через а обозначен первый вариант тензора напряжения  По (4.12.3), ограничиваясь только основными полиномами (4.11.1), имеем
По (4.12.3), ограничиваясь только основными полиномами (4.11.1), имеем

Более точная оценка по формуле (4.12.5) дает

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
- § 1. Поле напряжений в сплошной среде
- 1.2. Внешние силы.
- 1.3. Внутренние силы в сплошной среде.
- 1.4. Равновесие элементарного тетраэдра.
- 1.5. Необходимые условия равновесия сплошной среды.
- 1.6. Тензор функций напряжений.
- § 2. Свойства тензора напряжений
- 2.2. Круги Мора.
- 2.3. Разбиение тензора напряжений на шаровой тензор и девиатор.
- 2.4. Примеры напряженных состояний.
- § 3. Материальные координаты
- 3.2. Зависимости Коши.
- 3.3. Необходимые условия равновесия.
- 3.4. Другое определение тензора напряжений.
- 3.5. Элементарная работа внешних сил.
- 3.7. Инварианты тензора напряжений.
- § 4. Интегральные оценки напряженного состояния
- ГЛАВА II. ДЕФОРМАЦИЯ СПЛОШНОЙ СРЕДЫ
- § 1. Линейный тензор деформации
- 1.2. Определение линейного тензора деформации.
- § 2. Определение вектора перемещения по линейному тензору деформации
- 2.2. Вектор перемещения. Формула Чезаро.
- 2.3. Пример. Температурное поле.
- 2.4. Дисторсии Вольтерра.
- § 3. Первая мера и первый тензор конечной деформации
- 3.2. Тензоры-градиенты
- 3.3. Первая мера деформации (Коши—Грим).
- 3.4. Геометрическое значение компонент первой меры деформации.
- 3.5. Изменение ориентированной площадки.
- 3.6. Первый тензор конечной деформации.
- 3.7. Главные деформации, главные оси деформации.
- 3.8. Конечный поворот среды как твердого тела.
- 3.9. Выражение тензора конечной деформации через линейный тензор деформации и линейный вектор поворота.
- § 4. Вторая мера и второй тензор конечной деформации
- 4.2. Геометрическое значение компонент второй меры деформации.
- 4.3. Второй тензор конечной деформации (Альманзи—Гамель).
- § 5. Связь между мерами деформации
- 5.2. Связь между инвариантами.
- 5.3. Представление мер деформации в главных осях.
- 5.4. Инварианты тензоров конечной деформации.
- 5.5. Объемное расширение.
- 5.6. Преобразование подобия начального состояния.
- 5.7. Определение вектора перемещения по мерам деформации.
- § 6. Примеры деформированных состояний
- 6.2. Плоское поле перемещений.
- 6.3. Простой сдвиг.
- 6.4. Кручение круглого цилиндра.
- 6.5. Цилиндрический изгиб прямоугольной плиты.
- 6.6. Радиально-симметричная деформация полой сферы.
- 6.7. Осесимметричная деформация полого цилиндра.
- ЧАСТЬ II. УРАВНЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ
- ГЛАВА III. ЗАКОН СОСТОЯНИЯ ЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ
- 1.2. Элементарная работа.
- 1.3. Изотропная однородная среда Генки.
- § 2. Потенциальная энергия деформации
- 2.2. Изотермический процесс деформирования.
- 2.3. Адиабатический процесс.
- 2.4. Удельная энергия деформации. Среды Генки.
- § 3. Обобщенный закон Гука
- 3.2. Удельная потенциальная энергия деформации линейноупругого тела.
- 3.3. Формула Клапейрона. Область значений модулей упругости.
- 3.4. Учет температурных слагаемых. Свободная энергия.
- 3.5. Термодинамический потенциал Гиббса.
- 3.6. Уравнение теплопроводности.
- ГЛАВА IV. ОСНОВНЫЕ СООТНОШЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ
- § 1. Дифференциальные уравнения линейной теории упругости
- 1.3. Дифференциальные уравнения теории упругости в перемещениях.
- 1.4. Представление решения в форме Папковича — Нейбера.
- 1.5. Решение в напряжениях. Зависимости Бельтрами.
- 1.6. Преобразование Ю. А. Круткова.
- 1.7. Решение Буссинека-Галеркина.
- 1.8. Криволинейные координаты.
- 1.9. Ортогональные координаты.
- 1.10. Аксиально-симметричные задачи. Решение Лява.
- 1.11. Кручение тела вращения.
- 1.12. Деформация тела вращения.
- 1.13. Решение Папковича-Нейбера для тел вращения.
- 1.14. Учет температурных слагаемых.
- § 2. Вариационные принципы статики линейно-упругого тела
- 2.2. Принцип минимума потенциальной энергии системы.
- 2.3. Метод Ритца.
- 2.4. Способ Галеркина (1915).
- 2.5. Принцип минимума дополнительной работы.
- 2.6. Смешанный принцип стационарности (Е. Рейсснер, 1961).
- 2.7. Вариационные принципы при учете температурных слагаемых.
- 2.8. Принцип Сен-Венана. Энергетическое рассмотрение.
- § 3. Теорема взаимности. Потенциалы теории упругости
- 3.2. Тензор влияния. Теорема Максвелла.
- 3.3. Применение теоремы взаимности.
- 3.4. Теорема взаимности при учете температурных слагаемых.
- 3.5. Тензор влияния в неограниченной упругой среде.
- 3.6. Потенциалы теории упругости.
- 3.7. Определение поля перемещений по заданию внешних сил и вектора перемещения на поверхности тела.
- 3.8. О поведении потенциалов теории упругости на бесконечности.
- § 4. Теоремы единственности и существования решений
- 4.2. Интегральные уравнения первой краевой задачи.
- 4.3. Интегральные уравнения второй краевой задачи.
- 4.4. Сопоставление интегральных уравнений первой и второй краевых задач.
- 4.5. Теорема существования решения второй внешней и первой внутренней задачи.
- 4.6. Вторая внутренняя краевая задача.
- 4.7. Эластостатическая задача Робена.
- 4.8. Первая внешняя краевая задача
- § 5. Напряженное состояние в двусвязном объеме
- 5.2. Определение напряженного состояния по постоянным барьера.
- 5.3. Теорема взаимности.
- 5.4. Потенциальная энергия дисторсии.
- 5.5. Случай тела вращения.
- 5.6. Краевая задача для двусвязного тела вращения.
- ЧАСТЬ III. СПЕЦИАЛЬНЫЕ ЗАДАЧИ ЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ
- ГЛАВА V. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- 1.2. Система сил, распределенных в малом объеме. Формулы Лауричелла.
- 1.3. Интерпретация второго потенциала теории упругости.
- 1.4. Потенциалы Буссинека.
- 1.5. Термоупругие перемещения.
- 1.6. Напряженное состояние, создаваемое включением.
- § 2. Упругое полупространство
- 2.1. Задачи Буссинека и Черрути.
- 2.2. Частная задача Буссинека.
- 2.3. Распределенная нормальная нагрузка.
- 2.4. Применение функций Папковича-Нейбера к решению задачи Буссинека-Черрути.
- 2.5. Тензор влияния в упругом полупространстве.
- 2.6. Температурные напряжения в упругом полупространстве.
- 2.7. Случай установившейся температуры.
- 2.8. О вычислении потенциала простого слоя по плоской области.
- 2.9. Задача Дирихле для полупространства.
- 2.10. Первая краевая задача для полупространства.
- 2.11. Смешанные задачи для полупространства.
- 2.12. О принципе Сен-Венана. Формулировка Мизеса.
- 2.13. Сверхстатическая система сил.
- 2.14. Теоремы Стернберга (1954).
- § 3. Равновесие упругой сферы
- 3.2. Первая краевая задача.
- 3.3. Эластостатическая задача Робена для шара.
- 3.4. Тепловые напряжения в шаре.
- 3.5. Вторая краевая задача для сферы.
- 3.6. Вычисление вектора перемещения.
- 3.7. Напряженное состояние в центре шара.
- 3.9. Напряженное состояние в окрестности сферической полости.
- 3.10. Напряженное состояние в окрестности малой сферической полости в скрученном цилиндрическом стержне.
- 3.11. Действие массовых сил.
- 3.12. Гравитирующий шар.
- 3.13. Вращающийся шар.
- 3.14. Действие сосредоточенных сил.
- 3.15. Случай распределенной нагрузки.
- § 4. Тела вращения
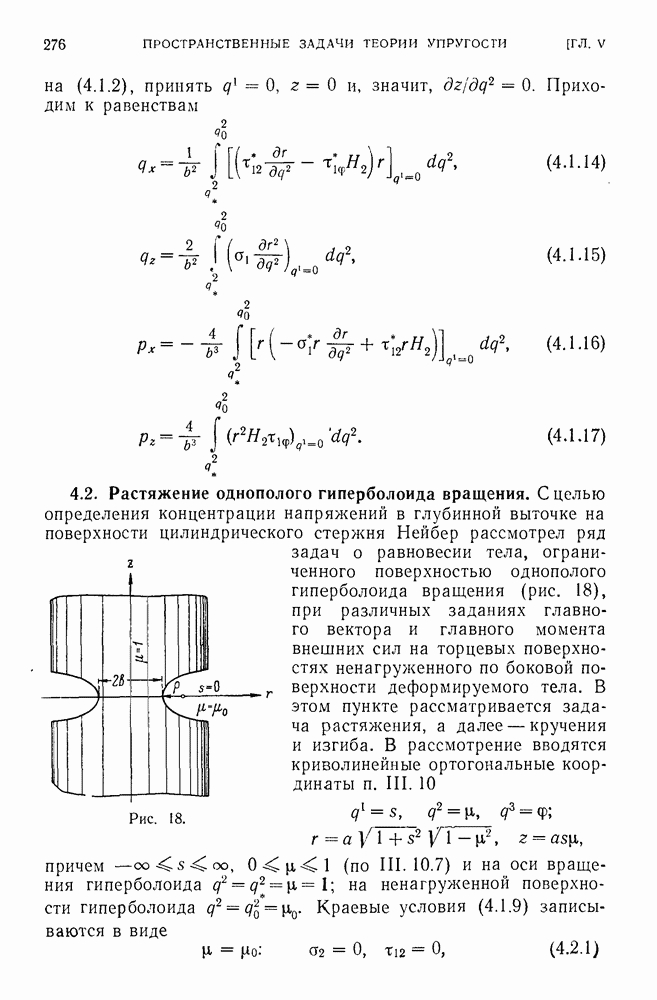
- 4.2. Растяжение однополого гиперболоида вращения.
- 4.3. Кручение гиперболоида.
- 4.4. Изгиб гиперболоида.
- 4.5. Вращающийся эллипсоид вращения.
- § 5. Эллипсоид
- 5.1. Эластостатическая задача Робена для трехосного эллипсоида.
- 5.3. Распределение напряжений по поверхности эллипсоида.
- 5.4. Перемещение поворота.
- 5.5. Распределение напряжений по поверхности эллипсоида.
- 5.6. Эллипсоидальная полость в неограниченной упругой среде.
- 5.7. Краевые условия.
- 5.8. Выражения постоянных через три параметра.
- 5.9. Сфероидальная полость в упругой среде.
- 5.10. Круговая щель в упругой среде.
- 5.11. Эллиптическая щель в упругой среде.
- § 6. Контактные задачи
- 6.1. Задача о жестком штампе. Краевое условие.
- 6.2. Способ решения задачи о жестком штампе.
- 6.2а. Представление сил и моментов, прилагаемых к неплоскому штампу.
- 6.3. Плоский, эллиптический в плане штамп.
- 6.4. Перемещения и напряжения.
- 6.5. Неплоский штамп.
- 6.5а. Определение сил и моментов, действующих на неплоский, эллиптический в плане штамп.
- 6.6. Перемещения и напряжения.
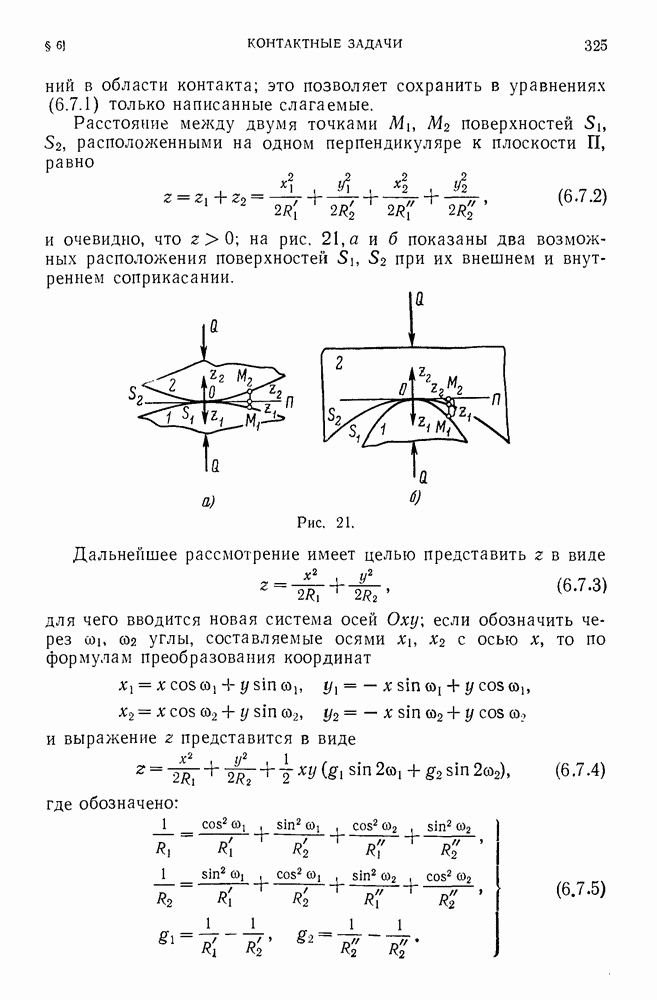
- 6.7. Соприкасание поверхностей.
- 6.8. Задача Герца о сжатии упругих тел.
- § 7. Равновесие упругого кругового цилиндра
- 7.2. Задача Ляме для полого цилиндра.
- 7.3. Дисторсии в полом цилиндре.
- 7.4. Полиномиальные решения задачи о равновесии цилиндра.
- 7.5. Кручение полого цилиндра силами, распределенными по торцу.
- 7.6. Решения в бесселевых функциях.
- 7.7. Задача Файлона.
- 7.8. Однородные решения.
- 7.9. Краевые условия на торцах.
- 7.10. Обобщенная ортогональность.
- ГЛАВА VI. ЗАДАЧА СЕН-ВЕНАНА
- 1.1. Постановка задачи Сен-Венана.
- 1.2. Интегральные уравнения равновесия.
- 1.3. Основные предположения.
- 1.4. Нормальное напряжение в задаче Сен-Венана.
- 1.5. Касательные напряжения
- § 2. Приведение к краевым задачам для уравнений Лапласа и Пуассона
- 2.2. Перемещения в задаче Сен-Венана.
- 2.3. Упругая линия.
- 2.4. Классификация задач Сен-Венана.
- 2.5. Определение постоянной а.
- 2.6. Центр жесткости.
- 2.7. Элементарные решения.
- § 3. Задача о кручении
- 3.2. Перемещения.
- 3.3. Теорема о циркуляции касательных напряжений.
- 3.4. Жесткость при кручении.
- 3.5. Мембранная аналогия Прандтля (1904).
- 3.6. Кручение стержня эллиптического сечения.
- 3.7. Неравенства для жесткости при кручении.
- 3.8. Кручение стержня прямоугольного сечения.
- 3.9. Решения в конечном виде.
- 3.10. Двусвязная область.
- 3.11. Эллиптическое кольцо.
- 3.12. Эксцентрическое кольцо.
- 3.13. Вариационное определение функции напряжений.
- 3.14. Приближенное решение задачи кручения.
- 3.15. Удлиненные профили.
- 3.16. Кручение тонкостенной трубы.
- 3.17. Многосвязные области.
- § 4. Изгиб силой
- 4.2. Изгиб стержня эллиптического поперечного сечения.
- 4.3. Функция напряжений С. П. Тимошенко.
- 4.4. Прямоугольное поперечное сечение.
- 4.5. Вариационная формулировка задачи изгиба.
- 4.6. Центр жесткости.
- 4.7. Приближенные решения.
- 4.8. Авиационный профиль.
- § 5. Задача Мичелла
- 5.2. Распределение нормальных напряжений.
- 5.3. Растяжение стержня.
- 5.3а. Растяжение стержня силами постоянной интенсивности.
- 5.4. Касательные напряжения
- 5.5. Напряжения
- 5.6. Определение …
- 5.7. Изгиб тяжелого стержня.
- 5.8. Средние значения напряжений.
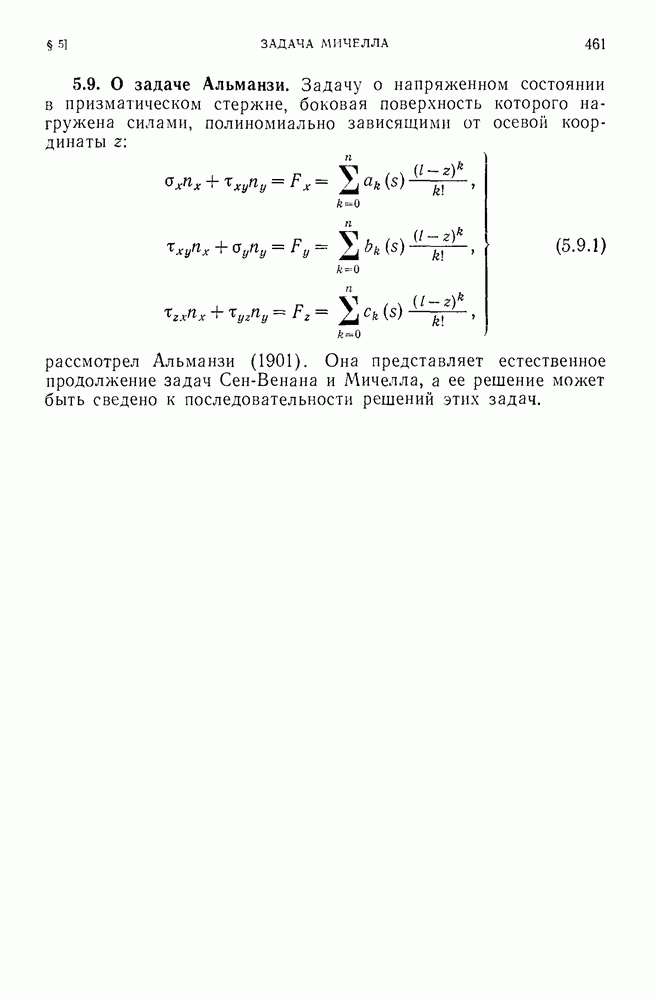
- 5.9. О задаче Альманзи.
- ГЛАВА VII. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
- 1.2. Функция напряжений Эри.
- 1.3. Дифференциальное уравнение для функции напряжений.
- 1.4. Плоское напряженное состояние.
- 1.5. Обобщенное плоское напряженное состояние.
- 1.6. Плоская задача.
- 1.7. Перемещения в плоской задаче.
- 1.8. Главный вектор и главный момент.
- 1.9. Ортогональные криволинейные координаты.
- 1.10. Полярные координаты на плоскости.
- 1.11. Представление бигармонической функции.
- 1.12. Введение комплексного переменного.
- 1.13. Преобразование формул плоской задачи.
- 1.14. Формула Гурса.
- 1.15. Перенос начала координат.
- § 2. Балка и брус с круговой осью
- 2.2. Плоская задача Сен-Венана.
- 2.3. Операторное представление решений.
- 2.4. Функция напряжений в задаче о полосе.
- 2.5. Элементарная теория балки.
- 2.6. Полиномиальное нагружение (Менаже, 1901).
- 2.7. Синусоидальное нагружение (решения Рибьера (1898) и Файлона (1903)).
- 2.8. Сосредоточенная сила (Карман и Зеевальд, 1927).
- 2.9. Брус с круговой осью, нагруженный по торцам (Головин, 1881).
- 2.10. Нагружение кругового бруса по поверхности.
- 2.11. Косинусоидальное нагружение.
- 2.12. Однородные решения.
- § 3. Упругая плоскость и полуплоскость
- 3.1. Сосредоточенная сила и сосредоточенный момент в упругой плоскости.
- 3.2. Задача Фламана (1892).
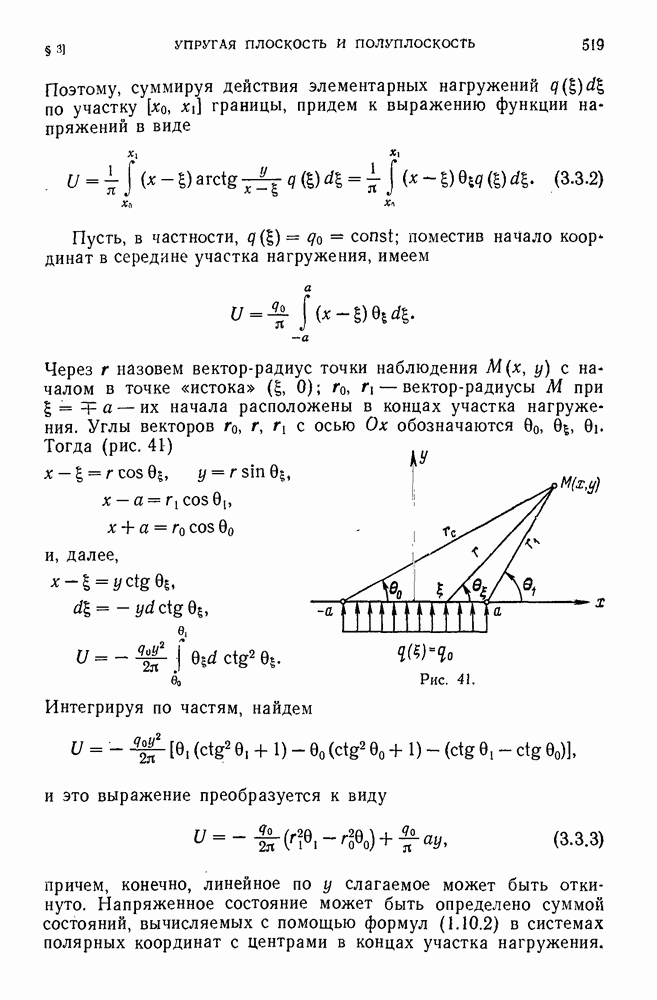
- 3.3. Общий случай нормального нагружения.
- 3.4. Нагружение силой, направленной вдоль границы.
- 3.5. Плоская контактная задача.
- 3.6. Построение потенциала w.
- 3.7. Плоский штамп.
- 3.8. Штамп параболического очертания.
- 3.9. Сосредоточенная сила в упругой полуплоскости.
- § 4. Упругий клин
- 4.1. Сосредоточенная сила в вершине клина.
- 4.2. Интегральное преобразование Меллина в задаче о клине.
- 4.3. Сосредоточенный момент в вершине клина.
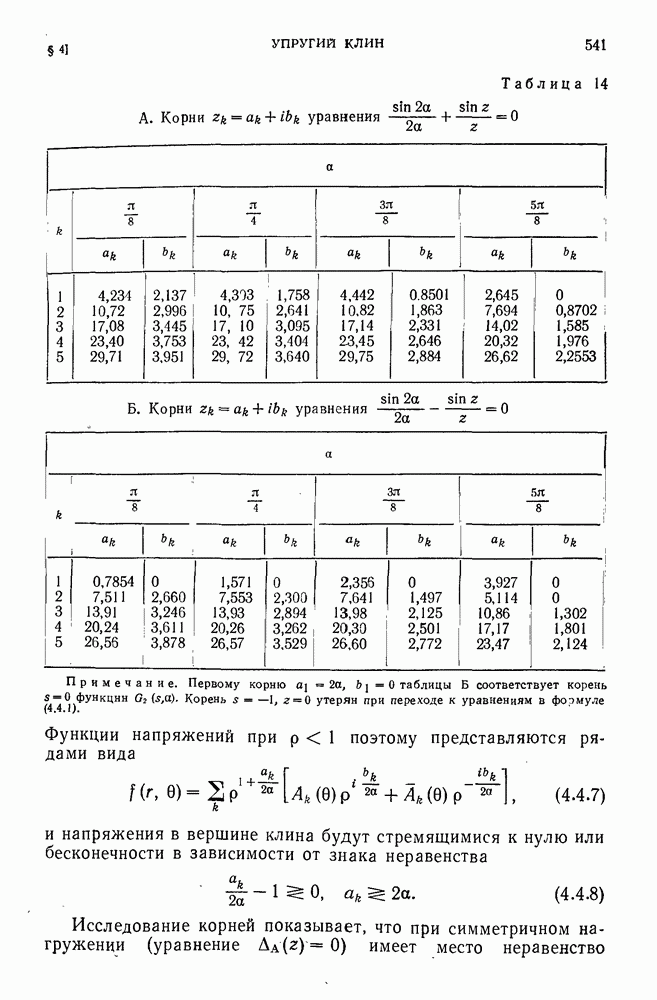
- 4.4. Нагружение боковых граней.
- § 5. Краевые задачи плоской теории упругости
- 5.2. Краевые задачи для односвязной конечной области.
- 5.3. Степень определенности функций Н. И. Мусхелишвили.
- 5.4. Бесконечная область с отверстием.
- 5.5. Двусвязная область. Дисторсия.
- 5.6. Представление функции напряжений в двусвязной области (Мичелл).
- 5.7. Тепловые напряжения. Плоская деформация.
- 5.8. Плоское напряженное состояние.
- 5.9. Стационарное распределение температуры.
- 5.10. Теорема Коши, интеграл Коши.
- 5.11. Интегралы типа Коши. Формулы Сохоцкого — Племели.
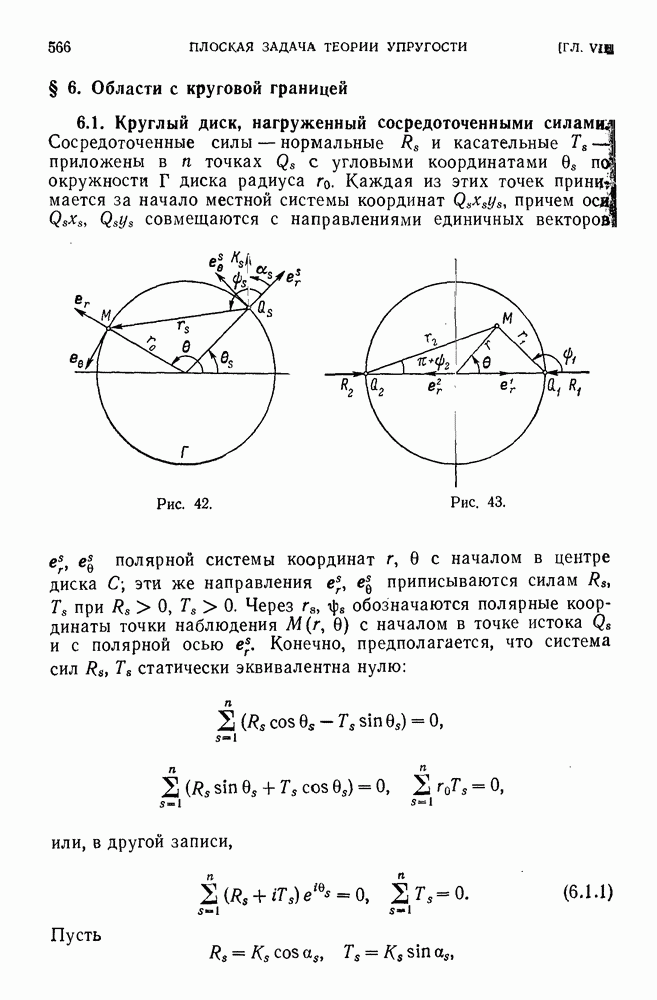
- § 6. Области с круговой границей
- 6.2. Общий случай нагружения круглого диска.
- 6.3. Способ интегралов Коши.
- 6.4. Нормальное напряжение на окружности.
- 6.5. Напряжения в центре диска.
- 6.6. Статически неуравновешенный вращающийся диск.
- 6.7. Первая краевая задача для круга.
- 6.8. Напряженное состояние.
- 6.9. Тепловые напряжения в диске, заключенном в жесткую обойму.
- 6.10. Круговое отверстие в бесконечной плоскости.
- 6.11. Равномерное нагружение края отверстия.
- 6.12. Растяжение плоскости, ослабленной круговым отверстием.
- 6.13. Продолжение Ф(z)
- 6.14. Решение краевых задач пп. 6.2, 6.10 способом продолжения.
- § 7. Круговое кольцо
- 7.2. Вторая краевая задача для кругового кольца.
- 7.3. Определение функций …
- 7.4. Труба под равномерным внешним и внутренним давлением (задача Ляме).
- 7.5. Температурные напряжения в кольце.
- 7.6. Растяжение кольца сосредоточенными силами.
- 7.7. Способ продолжения.
- § 8. Применение конформного преобразования
- 8.2. Способ интегралов Коши.
- 8.3. Эллиптическое отверстие.
- 8.4. Гипотрохоидное отверстие.
- 8.5. Односвязная конечная область.
- 8.6. Пример.
- 8.7. Первая краевая задача.
- 8.8. Эллиптическое отверстие.
- 8.9. Двусвязная область.
- 8.10. Неконцентрическое кольцо.
- ЧАСТЬ IV. ОСНОВНЫЕ СООТНОШЕНИЯ НЕЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ
- 1.1. Идеально-упругое тело.
- 1.2. Потенциалы деформации.
- 1.3. Однородное изотропное идеально-упругое тело.
- § 2. Закон состояния изотропного идеально-упругого тела
- 2.2. Начальное и натуральное состояния.
- 2.3. Связь между обобщенными модулями при различных начальных состояниях.
- 2.4. Представление тензора напряжений.
- 2.5. Выражение закона состояния через тензоры деформации.
- 2.6. Главные напряжения.
- 2.7. Выражение тензора напряжений.
- 2.8. Тензор напряжений Пиола (1836) — Кирхгоффа (1850).
- 2.9. О задании удельной потенциальной энергии деформации.
- § 3. Представление закона состояния квадратичным трехчленом
- 3.2. Представление энергетического тензора напряжений.
- 3.3. Представление тензора напряжений.
- 3.4. Разбиение тензора напряжений на шаровой тензор и девиатор.
- 3.5. Применение логарифмической меры деформации.
- § 4. Аппроксимации законов состояния
- 4.2. Зависимость коэффициентов квадратичного закона от начального состояния.
- 4.3. Знак удельной потенциальной энергии деформации.
- 4.4. Применение к задачам об одноосном растяжении.
- 4.5. Простой сдвиг.
- 4.6. Закон состояния Мурнагана.
- 4.7. Поведение материала при сверхвысоких давлениях.
- 4.8. Одноосное растяжение.
- 4.9. Несжимаемый материал.
- 4.10. Материалы с углом подобия девиаторов, равным нулю.
- § 5. Вариационные теоремы статики нелинейно-упругого тела
- 5.2. Стационарность потенциальной энергии системы.
- 5.3. Дополнительная работа деформации.
- 5.4. Стационарность дополнительной работы.
- 5.5. Удельная дополнительная работа деформации для полулинейного материала.
- ГЛАВА IX. ЗАДАЧИ И МЕТОДЫ НЕЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ
- 1.1. Тензор напряжений при аффинном преобразовании.
- 1.2. Всестороннее сжатие.
- 1.3. Одноосное растяжение.
- 1.4. Простой сдвиг.
- § 2. Упругий слой
- 2.2. Сжатие и растяжение упругой полосы.
- 2.3. Уравнения статики.
- 2.4. Сжатие слоя.
- 2.5. Растяжение слоя.
- § 3. Упругий цилиндр, упругая сфера
- 3.2. Напряжения.
- 3.3. Определение постоянных.
- 3.4. Материал Муни.
- 3.5. Цилиндр, «вывернутый наизнанку».
- 3.6. Кручение круглого цилиндра.
- 3.7. Напряжения, крутящий момент, осевая сила.
- 3.8. Симметричная деформация полого шара (задача Ляме для шара).
- 3.9. Несжимаемый материал.
- 3.10. Применение принципа стационарности потенциальной энергии.
- § 4. Малая деформация при наличии начального нагружения
- 4.2. Тензор напряжений.
- 4.3. Необходимые условия равновесия.
- 4.4. Представление тензора «тета».
- 4.5. Трехосное напряженное состояние.
- 4.6. Гидростатическое напряженное состояние.
- 4.7. Одноосное растяжение.
- 4.8. Деформация кручения сжатого стержня.
- § 5. Эффекты второго порядка
- 5.2. Уравнения равновесия.
- 5.3. Эффекты второго порядка.
- 5.3а. Изменение объема тела, подвергнутого дисторсии.
- 5.4. Выбор исходного приближения.
- 5.5. Эффекты второго порядка в задаче о кручении стержня.
- 5.6. Несжимаемая среда.
- 5.7. Уравнения равновесия.
- § 6. Плоская задача
- § 7. Полулинейный материал
- 7.2. Сохранение главных направлений.
- 7.3. Примеры (цилиндр и сфера).
- 7.4. Плоская деформация.
- 7.5. Напряженное состояние при плоском аффинном преобразовании.
- 7.6. Изгибание полосы в цилиндрическую панель.
- 7.7. Наложение малой деформации.
- 7.8. Случай сохранения главных направлений.
- 7.9. Уравнения нейтрального равновесия Саусвелла (1913).
- 7.10. Представление решений уравнений Саусвелла.
- 7.11. Бифуркация равновесия сжатого стержня.
- 7.12. Стержень круглого поперечного сечения.
- 7.13. Бифуркация равновесия полой сферы, сжатой равномерно распределенным давлением.
- ПРИЛОЖЕНИЕ I. ОСНОВЫ ТЕНЗОРНОЙ АЛГЕБРЫ
- 1.2. Символы Леви-Чивита.
- 1.3. Тензор второго ранга.
- 1.4. Простейшие операции с тензорами.
- 1.5. Диада векторов, диадное представление тензора второго ранга.
- 1.6. Тензоры высших рангов. Свертывание индексов.
- 1.7. Обратный тензор.
- 1.8. Тензор поворота.
- 1.9. Главные оси и главные значения симметричного тензора.
- 1.10. Выражение компонент тензора через главные значения. Инварианты. Теорема Кейли-Гамильтона.
- 1.10а. Главные оси и главные значения несимметричного тензора.
- 1.11. Разбиение симметричного тензора второго ранга на девиатор и шаровой тензор.
- 1.12. Функции тензоров.
- 1.13. Выделение шаровой и девиаторной частей.
- 1.14. Линейная связь между тензорами.
- ПРИЛОЖЕНИЕ II. ОСНОВНЫЕ ОПЕРАЦИИ ТЕНЗОРНОГО АНАЛИЗА
- II.2. Дифференциальные операции в векторном поле.
- II.3. Дифференциальные операции над тензорами.
- II.4. Двукратное дифференцирование.
- II.5. Преобразование объемного интеграла в поверхностный.
- II.6. Преобразование Стокса.
- ПРИЛОЖЕНИЕ III. ОРТОГОНАЛЬНЫЕ КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
- III.2. Квадрат линейного элемента.
- III.3. Ортогональная криволинейная система координат. Базисные векторы.
- III.4, Дифференцирование базисных векторов.
- III.5. Дифференциальные операции в ортогональных криволинейных координатах.
- III.6. Зависимости Ляме.
- III.7. Цилиндрические координаты.
- III.8. Сферические координаты.
- III.9. Тела вращения.
- III.10. Вырожденные эллиптические координаты.
- III.11. Эллиптические координаты (общий случай).
- ПРИЛОЖЕНИЕ IV. ТЕНЗОРНАЯ АЛГЕБРА В КОСОУГОЛЬНОМ БАЗИСЕ
- IV.2. Вектор в косоугольном базисе.
- IV.3. Метрический тензор.
- IV.4. Тензор Леви-Чивита.
- IV.5. Тензоры в косоугольном базисе.
- IV.6. Преобразование базиса.
- IV.7. Главные оси симметричного тензора. Главные инварианты.
- ПРИЛОЖЕНИЕ V. ОПЕРАЦИИ ТЕНЗОРНОГО АНАЛИЗА В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- V.2. Производные базисных векторов.
- V.3. Ковариантное дифференцирование.
- V.4. Дифференциальные операции в криволинейных координатах.
- V.5. Переход к ортогональным криволинейным координатам.
- V.6. Тензор Римана — Кристоффеля.
- V.7. Тензор …
- V.8. Преобразование поверхностного интеграла в объемный.
- ПРИЛОЖЕНИЕ VI. СВЕДЕНИЯ ПО ТЕОРИИ СФЕРИЧЕСКИХ И ЭЛЛИПСОИДАЛЬНЫХ ФУНКЦИЙ
- VI.2. Сферические функции Лапласа.
- VI.3. Решения …
- VI.4. Решение внешней и внутренней задач для шара.
- VI.5. Внешняя и внутренняя задачи Дирихле для сжатого эллипсоида (сфероида).
- VI.6. Представление гармонических полиномов произведениями Ляме.
- VI.7. Функция …
- VI.8. Потенциалы простого слоя на эллипсоиде.
- ЛИТЕРАТУРНЫЕ УКАЗАНИЯ