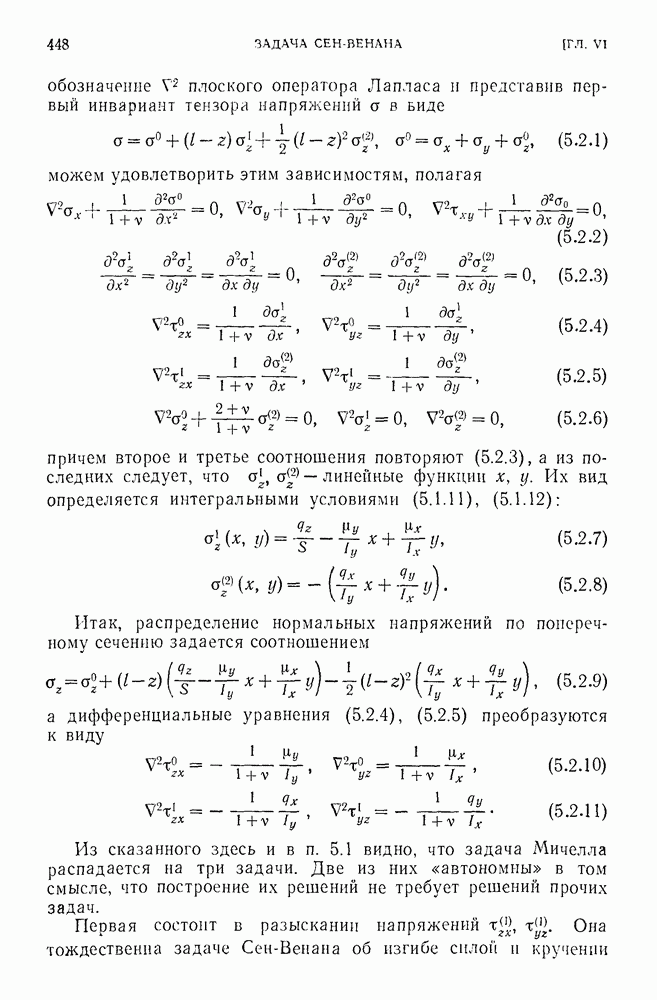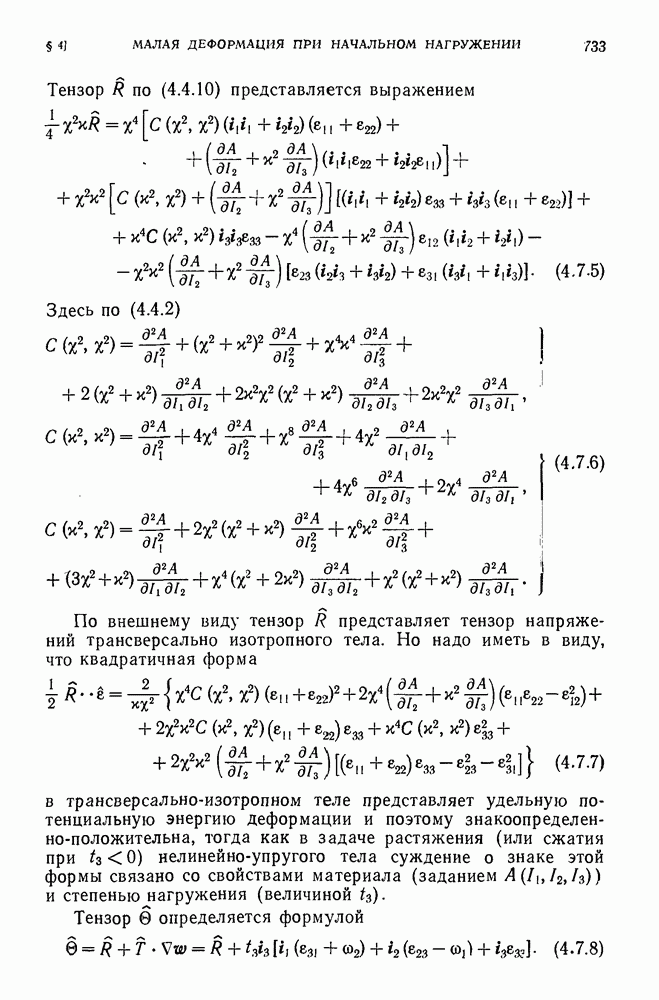| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 6. Плоская задача
6.1. Геометрические соотношения.
В состоянии плоской деформации координаты  точек среды связаны с их координатами
точек среды связаны с их координатами  в начальном состоянии зависимостями
в начальном состоянии зависимостями

Введя материальные координаты  имеем
имеем

причем здесь и в дальнейшем (пп. 6.1-6.9) греческие индексы принимают значения 1, 2 (латинские, как и ранее, — значения 1, 2, 3). Вектор-радиусы точки в начальном (v-объем) и в деформированном состояниях  -объем) равны
-объем) равны

и базисные векторы в этих состояниях будут

Ковариантные компоненты метрических тензоров  определяются теперь формулами
определяются теперь формулами

так что

Их контравариантные компоненты (отличные от нуля) равны

Этим в рассмотрение вводятся плоские метрические тензоры  и
и  -объемах:
-объемах:

причем векторы взаимных базисов определяются известными равенствами

В записи компонент тензоров Леви-Чивита  опускается третий индекс 3:
опускается третий индекс 3:

где

Пользуясь ими, можно переписать формулы (6.1.7) и им обратные в виде

Инварианты меры деформации  определяемые формулами (5.2.6) — (5.2.8) гл. II, равны
определяемые формулами (5.2.6) — (5.2.8) гл. II, равны

Сославшись на (6.1.12), имеем

Но нетрудно, пользуясь определениями (6.1.11), проверить соотношения

Поэтому

чем устанавливается соотношение, связывающее инварианты:

6.2. Уравнение состояния.
Удельная потенциальная энергия деформации далее рассматривается как функция инвариантов 

так что

Уравнение состояния (2.1.9) гл. VIII может быть записано в виде

и по 

Заменив инвариант  его значением (6.1.13) и используя (6.2.2), имеем, далее,
его значением (6.1.13) и используя (6.2.2), имеем, далее,

При фиксированных  возможны четыре сочетания значений
возможны четыре сочетания значений 

Поэтому (не суммировать по 

так что по (6.1.6), (6.1.7)

и, возвращаясь к (6.2.4), (6.2.2), имеем

Для несжимаемой среды

так что

где  наперед неизвестная функция координат.
наперед неизвестная функция координат.
6.3. Уравнения статики.
При отсутствии массовых сил уравнения равновесия в объеме записываются в виде
Но  не зависят от
не зависят от  поэтому последнее уравнение тождественно удовлетворяется, а первая группа уравнений записывается в виде
поэтому последнее уравнение тождественно удовлетворяется, а первая группа уравнений записывается в виде

или

причем символы Кристоффеля вычисляются по метрическому тензору В.
Уравнения равновесия на поверхности могут быть записаны в одной из форм (3.3.7) или (3.3.8) гл. I:

причем  ковариантные компоненты единичных векторов внешних нормалей
ковариантные компоненты единичных векторов внешних нормалей  к контурам у,
к контурам у,  поперечного сечения тела в начальном и соответственно в деформированном состояниях тела:
поперечного сечения тела в начальном и соответственно в деформированном состояниях тела:

Через обозначены контравариантные компоненты поверхностной силы:

6.4. Функция напряжений.
Тензор функций напряжений (п. 1.6 гл. I) задается в виде
а тензор напряжений определяется по нему равенством (1.6.6) гл. I:

Здесь не рассматривается независимо определяемая по (6.2.3) компонента 
Вычисление проводится так:

По условию обращения в нуль ковариантной производной тензора Леви-Чивита

имеем, изменив наименования немых индексов,

и подстановка в (6.4.2) приводит к следующему представлению тензора напряжений:

Величина в скобках представляет ковариантную производную ковариантных компонент градиента 

Итак,

Обратные соотношения имеют вид

и по 

Выражение первого инварианта тензора напряжений представляется в виде

Как и следовало ожидать, он оказался равным лапласиану над  (в метрике деформированного тела):
(в метрике деформированного тела):

Единичные векторы касательной  и нормали
и нормали  плоской кривой
плоской кривой  в деформированном теле
в деформированном теле

определяются, в предположении, что  ориентированы, как оси
ориентированы, как оси  по формулам
по формулам

Вектор напряжения, передаваемого частью среды «над  » (куда направлен вектор
» (куда направлен вектор  на среду, расположенную «под
на среду, расположенную «под  », равен
», равен

Вместе с тем, как указывалось выше,

и поэтому

Этой формулой определен главный вектор напряжений  по дуге
по дуге  кривой
кривой  его можно представить также в виде
его можно представить также в виде

так что

Это — обобщение формул (1.8.4) гл. VII. В них  — контравариантные компоненты главного вектора напряжений в метрике деформированного тела.
— контравариантные компоненты главного вектора напряжений в метрике деформированного тела.
Главный момент напряжений на дуге кривой  относительно начала координат в плоскости
относительно начала координат в плоскости  представляется интегралом
представляется интегралом

Обратившись к соотношению

приходим к такому выражению главного момента относительно оси 

Здесь дано обобщение формулы (1.8.5) гл. VII.
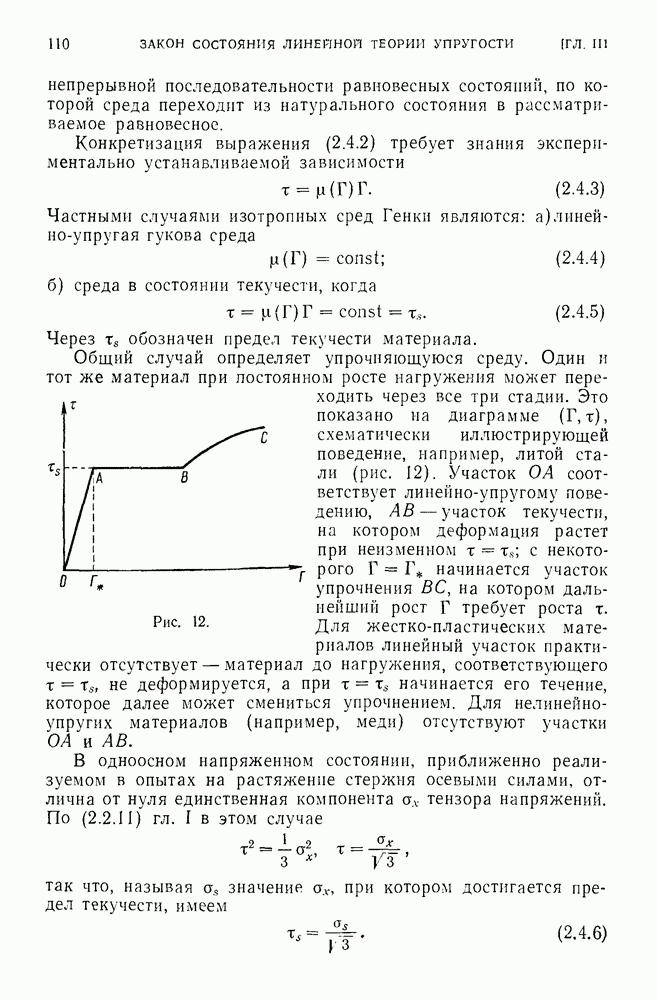
6.5. Плоское напряженное состояние.
Рассматривается тело, имеющее в начальном состоянии (v-объем) форму плиты малой по сравнению с ее размерами в плане постоянной толщины  Торцы плиты не нагружены, а поверхностные силы на ее боковой поверхности параллельны срединной плоскости плиты
Торцы плиты не нагружены, а поверхностные силы на ее боковой поверхности параллельны срединной плоскости плиты  и распределены симметрично относительно этой плоскости. Предполагается, что они сохраняют эти свойства (параллельность и симметричность относительно срединной плоскости) в деформированной плите (V-объем), так что напряженное состояние в ней симметрично относительно срединной плоскости
и распределены симметрично относительно этой плоскости. Предполагается, что они сохраняют эти свойства (параллельность и симметричность относительно срединной плоскости) в деформированной плите (V-объем), так что напряженное состояние в ней симметрично относительно срединной плоскости 
Материальные координаты  вводятся соотношениями
вводятся соотношениями 
Поэтому векторы исходного и взаимного базисов в  -объеме равны
-объеме равны

и ко- и контравариантные компоненты метрического тензора  -объема
-объема  определяются формулами (6.1.5), (6.1.7).
определяются формулами (6.1.5), (6.1.7).

Единичный вектор нормали  к площадке
к площадке  сонаправленный с вектором
сонаправленный с вектором  взаимного базиса, определяется по формуле
взаимного базиса, определяется по формуле

Поэтому вектор напряжений на этой площадке  равен
равен

а их главный вектор по толщине плиты, обозначаемый  будет
будет

Введя обозначения

и замечая, что  вследствие симметрии напряженного состояния, нечетны по
вследствие симметрии напряженного состояния, нечетны по 

приходим к формулам

Функции  можно рассматривать как контравариантные компоненты поверхностного симметричного тензора
можно рассматривать как контравариантные компоненты поверхностного симметричного тензора

На поверхности  ограничивающей деформированную плиту,
ограничивающей деформированную плиту,

и векторы  (отличные от базисных векторов
(отличные от базисных векторов 

расположены в ее касательной плоскости, а вектор


сонаправлен с единичным вектором нормали  к ней. Замечай, что
к ней. Замечай, что

получаем

Условие отсутствия нагружения на этой поверхности принимает вид

Из получающихся трех соотношений

исключаются компоненты  тензора напряжений. Приходим к уравнению:
тензора напряжений. Приходим к уравнению:

6.6. Уравнения равновесия.
Уравнения статики в объеме при отсутствии объемных сил, записываемые в виде

интегрируются по толщине плиты. Приходим к равенству

Пределы интеграла зависят от  поэтому
поэтому

и равенство (6.6.1) записывается в виде

Величина в квадратных скобках по (6.5.12) обращается в нуль. Обратившись теперь к формулам (6.5.6), (6.5.7), приходим к уравнению равновесия, в которое входят только величины, определяемые на средней поверхности:

Они целиком повторяют уравнения статики (6.3.1) задачи о плоской деформации. Поэтому им можно удовлетворить, введя в рассмотрение функцию напряжений  так что по (6.4.4)
так что по (6.4.4)

На боковой поверхности деформированной плиты

где  — дуга кривой
— дуга кривой  ограничивающей поперечное сечение в срединной плоскости
ограничивающей поперечное сечение в срединной плоскости  Векторы
Векторы

расположены в касательной плоскости этой поверхности, а вектор

сонаправлен с нормалью к ней; это — единичный вектор нормали, так как

Здесь использована формула (6.1.12) и учтено, что

Поверхностная сила  на поверхности (6.6.4) определяется равенством
на поверхности (6.6.4) определяется равенством

или

Главный вектор этих сил по толщине плиты по (6.5.6), (6.5.7) равен

Пришли к равенству (6.4.10); из него, повторив сказанное в п. 6.4, можно получить краевые условия (6.4.13), (6.4.14) для функции напряжений 
6.7. Уравнение состояния.
Вследствие предположенной симметрии деформации относительно плоскости  декартовы координаты точки
декартовы координаты точки  в начальном состоянии плиты четны,
в начальном состоянии плиты четны,  нечетна по
нечетна по  Поэтому
Поэтому

где X — неизвестная функция 
Эти соотношения позволяют записать выражения компонент метрического тензора  определителя
определителя  в виде (6.1.5), (6.1.7):
в виде (6.1.5), (6.1.7):

Повторив вычисление п. 6.1, приходим также к выражениям (6.1.13), (6.1.15) инвариантов меры деформации 

и к соотношению связи между ними (6.1.16). Это позволяет записать в форме (6.2.3), (6.2.5) выражения компонент тензора напряжения на срединной плоскости:

В случае несжимаемой среды приходим к формулам (6.2 7), (6.2.8). Для весьма тонкой пластинки в соответствии с (6.7.1) имеем

и при 

При этой степени точности связь компонент  тензора напряжений на срединной плоскости с компонентами осредненных внутренних усилий может быть определена из соотношения
тензора напряжений на срединной плоскости с компонентами осредненных внутренних усилий может быть определена из соотношения

так что

По (6.5.13), (6.7.5) имеем также

и при  можно принять
можно принять

6.8. Система уравнений задачи о плоском напряженном состоянии.
В предположении малости толщины плиты задача о напряженном состоянии при симметричном нагружении ее боковой поверхности сведена к рассмотрению величин на срединной плоскости. Разыскивается не тензор напряжений, а усредненные значения  основных напряжений
основных напряжений  тогда как остальные компоненты
тогда как остальные компоненты  этого тензора, вследствие их малости сравнительно с основными, исключены из рассмотрения.
этого тензора, вследствие их малости сравнительно с основными, исключены из рассмотрения.
Две группы соотношений, определяющих симметричный тензор осредненных напряжений, сводятся к уравнению статики

и к уравнениям состояния

Здесь  функция инвариантов
функция инвариантов 

представляющая выражение удельной потенциальной энергии деформации  из которого инвариант
из которого инвариант  исключен с помощью соотношения
исключен с помощью соотношения

Дополнительное условие, служащее для определения неизвестной функции  выражает требование отсутствия напряжения
выражает требование отсутствия напряжения  на срединной поверхности:
на срединной поверхности:

Краевое условие на контуре  сечении плиты срединной плоскостью — представляется соотношением
сечении плиты срединной плоскостью — представляется соотношением

где  главный вектор поверхностных сил на боковой поверхности:
главный вектор поверхностных сил на боковой поверхности:

Уравнениям статики можно удовлетворить, выражая напряжения через функцию напряжений 

Обратные соотношения имеют вид

Краевые условия для функции напряжений даются формулами (6.4.11) — (6.4.14).
В случае несжимаемого тела

и неизвестная скалярная функция  вводимая вместо
вводимая вместо  определяется из уравнений статики, дополненных этим условием.
определяется из уравнений статики, дополненных этим условием.
6.9. Применение логарифмической меры в задаче о плоской деформации.
В плоском поле перемещений (6.2.1) гл. II главные значения тензоров  или
или  равны
равны  (см. п. 3.5 гл. VIII). Через х обозначается угол поворота, совмещающего оси
(см. п. 3.5 гл. VIII). Через х обозначается угол поворота, совмещающего оси  с главными осями
с главными осями  тензора
тензора 

Эти оси совмещаются с осями  тензора
тензора  поворотом на угол
поворотом на угол  , так что
, так что

Вместе с тем по (3.4.5) гл. II имеем

или

Приходим к соотношениям

позволяющим выразить величины  через четыре инвариантных параметра
через четыре инвариантных параметра 

Эти параметры связаны условиями интегрируемости

Заметим также, что представления компонент тензора  в осях OXYZ даются формулами [см., например, (1.3.14)]
в осях OXYZ даются формулами [см., например, (1.3.14)]

а соосная с  логарифмическая мера деформации
логарифмическая мера деформации  определяется ее компонентами
определяется ее компонентами

В случае плоской деформации несжимаемого материала  и эти выражения упрощаются:
и эти выражения упрощаются:

а величины  представляются в виде
представляются в виде

Компоненты тензора напряжений  для несжимаемого материала с равной нулю фазой подобия и согласно (3.5.14) гл. VIII и (6.9.4) оказываются равными
для несжимаемого материала с равной нулю фазой подобия и согласно (3.5.14) гл. VIII и (6.9.4) оказываются равными

Для определения четырех неизвестных параметров имеется такое же число уравнений — два уравнения статики и два условия интегрируемости (6.9.2).
6.10. Плоская деформация несжимаемого материала с равной нулю фазой подобия девиаторов.
Уравнения статики при отсутствии массовых сил можно записать в виде

За независимые переменные приняты координаты точки в деформированном состоянии тела. Обратившись к формулам (6.9.6), получим

Этому соотношению можно удовлетворить, полагая

и, поскольку  вещественно, надо принять, введя вещественную функцию
вещественно, надо принять, введя вещественную функцию 

Приходим к соотношениям, которые можно было предвидеть:

и функция  оказалась, конечно, функцией Эри плоской задачи:
оказалась, конечно, функцией Эри плоской задачи:

Следствием первого соотношения (6.10.3) является формула, связывающая величину  с функцией напряжений:
с функцией напряжений:

Из нее можно определить производные  по
по 

Из того же соотношения (6.10.3) имеем

и, далее, учитывая (6.10.5), (6.10.6),

и аналогичное уравнение для производной по 
Возвращаясь к соотношениям (6.9.5), представим их в виде

причем  Из них находим обратные соотношения
Из них находим обратные соотношения

Записав условия их интегрируемости

придем к двум уравнениям:

В них следует заменить величины

их значениями по (6.10.6) — (6.10.8). Это позволит выразить производные от а по  через производные функции напряжений и величину
через производные функции напряжений и величину  (параметр а исключен). Вслед за этим условие интегрируемости
(параметр а исключен). Вслед за этим условие интегрируемости

приведет к дифференциальному уравнению четвертого порядка для функции напряжений  в которое войдет также величина
в которое войдет также величина  Но последняя связана с
Но последняя связана с  соотношением (6.10.5).
соотношением (6.10.5).
Переход к исходным независимым переменным  , осуществляется с помощью соотношений
, осуществляется с помощью соотношений

с последующей заменой производных вида (6.10.12) их значениями.
Не останавливаемся на не представляющих затруднений записях краевых условий.
6.11. Пример. Радиально-симметричная деформация.
При такой деформации

причем  - вещественная функция. По (6.10.9) имеем
- вещественная функция. По (6.10.9) имеем

так что 

Отсюда находим

и далее

так что  где
где  радиус отверстия в деформируемом цилиндрическом теле.
радиус отверстия в деформируемом цилиндрическом теле.
Теперь, сославшись, например, на формулу (1.13.8) гл. VII, по (6.10.3) и (6.11.2) имеем

и, далее,

Здесь, как и выше, штрихом обозначается производная по  Теперь находим
Теперь находим

и дифференциальное уравнение равновесия (6.11.5) приводится к виду

После замены  его значением по (6.11.4)
его значением по (6.11.4)

и введения новой независимой переменной (вместо 

приходим к легко интегрируемому дифференциальному уравнению относительно 

Из него имеем

после чего по  определяется и далее то есть по
определяется и далее то есть по  - сумма нормальных напряжений, а значит, и каждое из напряжений
- сумма нормальных напряжений, а значит, и каждое из напряжений  Не останавливаемся на этом вычислении и на определении постоянных по краевому условию.
Не останавливаемся на этом вычислении и на определении постоянных по краевому условию.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ЧАСТЬ I. ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
- § 1. Поле напряжений в сплошной среде
- 1.2. Внешние силы.
- 1.3. Внутренние силы в сплошной среде.
- 1.4. Равновесие элементарного тетраэдра.
- 1.5. Необходимые условия равновесия сплошной среды.
- 1.6. Тензор функций напряжений.
- § 2. Свойства тензора напряжений
- 2.2. Круги Мора.
- 2.3. Разбиение тензора напряжений на шаровой тензор и девиатор.
- 2.4. Примеры напряженных состояний.
- § 3. Материальные координаты
- 3.2. Зависимости Коши.
- 3.3. Необходимые условия равновесия.
- 3.4. Другое определение тензора напряжений.
- 3.5. Элементарная работа внешних сил.
- 3.7. Инварианты тензора напряжений.
- § 4. Интегральные оценки напряженного состояния
- ГЛАВА II. ДЕФОРМАЦИЯ СПЛОШНОЙ СРЕДЫ
- § 1. Линейный тензор деформации
- 1.2. Определение линейного тензора деформации.
- § 2. Определение вектора перемещения по линейному тензору деформации
- 2.2. Вектор перемещения. Формула Чезаро.
- 2.3. Пример. Температурное поле.
- 2.4. Дисторсии Вольтерра.
- § 3. Первая мера и первый тензор конечной деформации
- 3.2. Тензоры-градиенты
- 3.3. Первая мера деформации (Коши—Грим).
- 3.4. Геометрическое значение компонент первой меры деформации.
- 3.5. Изменение ориентированной площадки.
- 3.6. Первый тензор конечной деформации.
- 3.7. Главные деформации, главные оси деформации.
- 3.8. Конечный поворот среды как твердого тела.
- 3.9. Выражение тензора конечной деформации через линейный тензор деформации и линейный вектор поворота.
- § 4. Вторая мера и второй тензор конечной деформации
- 4.2. Геометрическое значение компонент второй меры деформации.
- 4.3. Второй тензор конечной деформации (Альманзи—Гамель).
- § 5. Связь между мерами деформации
- 5.2. Связь между инвариантами.
- 5.3. Представление мер деформации в главных осях.
- 5.4. Инварианты тензоров конечной деформации.
- 5.5. Объемное расширение.
- 5.6. Преобразование подобия начального состояния.
- 5.7. Определение вектора перемещения по мерам деформации.
- § 6. Примеры деформированных состояний
- 6.2. Плоское поле перемещений.
- 6.3. Простой сдвиг.
- 6.4. Кручение круглого цилиндра.
- 6.5. Цилиндрический изгиб прямоугольной плиты.
- 6.6. Радиально-симметричная деформация полой сферы.
- 6.7. Осесимметричная деформация полого цилиндра.
- ЧАСТЬ II. УРАВНЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ
- ГЛАВА III. ЗАКОН СОСТОЯНИЯ ЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ
- 1.2. Элементарная работа.
- 1.3. Изотропная однородная среда Генки.
- § 2. Потенциальная энергия деформации
- 2.2. Изотермический процесс деформирования.
- 2.3. Адиабатический процесс.
- 2.4. Удельная энергия деформации. Среды Генки.
- § 3. Обобщенный закон Гука
- 3.2. Удельная потенциальная энергия деформации линейноупругого тела.
- 3.3. Формула Клапейрона. Область значений модулей упругости.
- 3.4. Учет температурных слагаемых. Свободная энергия.
- 3.5. Термодинамический потенциал Гиббса.
- 3.6. Уравнение теплопроводности.
- ГЛАВА IV. ОСНОВНЫЕ СООТНОШЕНИЯ ЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ
- § 1. Дифференциальные уравнения линейной теории упругости
- 1.3. Дифференциальные уравнения теории упругости в перемещениях.
- 1.4. Представление решения в форме Папковича — Нейбера.
- 1.5. Решение в напряжениях. Зависимости Бельтрами.
- 1.6. Преобразование Ю. А. Круткова.
- 1.7. Решение Буссинека-Галеркина.
- 1.8. Криволинейные координаты.
- 1.9. Ортогональные координаты.
- 1.10. Аксиально-симметричные задачи. Решение Лява.
- 1.11. Кручение тела вращения.
- 1.12. Деформация тела вращения.
- 1.13. Решение Папковича-Нейбера для тел вращения.
- 1.14. Учет температурных слагаемых.
- § 2. Вариационные принципы статики линейно-упругого тела
- 2.2. Принцип минимума потенциальной энергии системы.
- 2.3. Метод Ритца.
- 2.4. Способ Галеркина (1915).
- 2.5. Принцип минимума дополнительной работы.
- 2.6. Смешанный принцип стационарности (Е. Рейсснер, 1961).
- 2.7. Вариационные принципы при учете температурных слагаемых.
- 2.8. Принцип Сен-Венана. Энергетическое рассмотрение.
- § 3. Теорема взаимности. Потенциалы теории упругости
- 3.2. Тензор влияния. Теорема Максвелла.
- 3.3. Применение теоремы взаимности.
- 3.4. Теорема взаимности при учете температурных слагаемых.
- 3.5. Тензор влияния в неограниченной упругой среде.
- 3.6. Потенциалы теории упругости.
- 3.7. Определение поля перемещений по заданию внешних сил и вектора перемещения на поверхности тела.
- 3.8. О поведении потенциалов теории упругости на бесконечности.
- § 4. Теоремы единственности и существования решений
- 4.2. Интегральные уравнения первой краевой задачи.
- 4.3. Интегральные уравнения второй краевой задачи.
- 4.4. Сопоставление интегральных уравнений первой и второй краевых задач.
- 4.5. Теорема существования решения второй внешней и первой внутренней задачи.
- 4.6. Вторая внутренняя краевая задача.
- 4.7. Эластостатическая задача Робена.
- 4.8. Первая внешняя краевая задача
- § 5. Напряженное состояние в двусвязном объеме
- 5.2. Определение напряженного состояния по постоянным барьера.
- 5.3. Теорема взаимности.
- 5.4. Потенциальная энергия дисторсии.
- 5.5. Случай тела вращения.
- 5.6. Краевая задача для двусвязного тела вращения.
- ЧАСТЬ III. СПЕЦИАЛЬНЫЕ ЗАДАЧИ ЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ
- ГЛАВА V. ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- 1.2. Система сил, распределенных в малом объеме. Формулы Лауричелла.
- 1.3. Интерпретация второго потенциала теории упругости.
- 1.4. Потенциалы Буссинека.
- 1.5. Термоупругие перемещения.
- 1.6. Напряженное состояние, создаваемое включением.
- § 2. Упругое полупространство
- 2.1. Задачи Буссинека и Черрути.
- 2.2. Частная задача Буссинека.
- 2.3. Распределенная нормальная нагрузка.
- 2.4. Применение функций Папковича-Нейбера к решению задачи Буссинека-Черрути.
- 2.5. Тензор влияния в упругом полупространстве.
- 2.6. Температурные напряжения в упругом полупространстве.
- 2.7. Случай установившейся температуры.
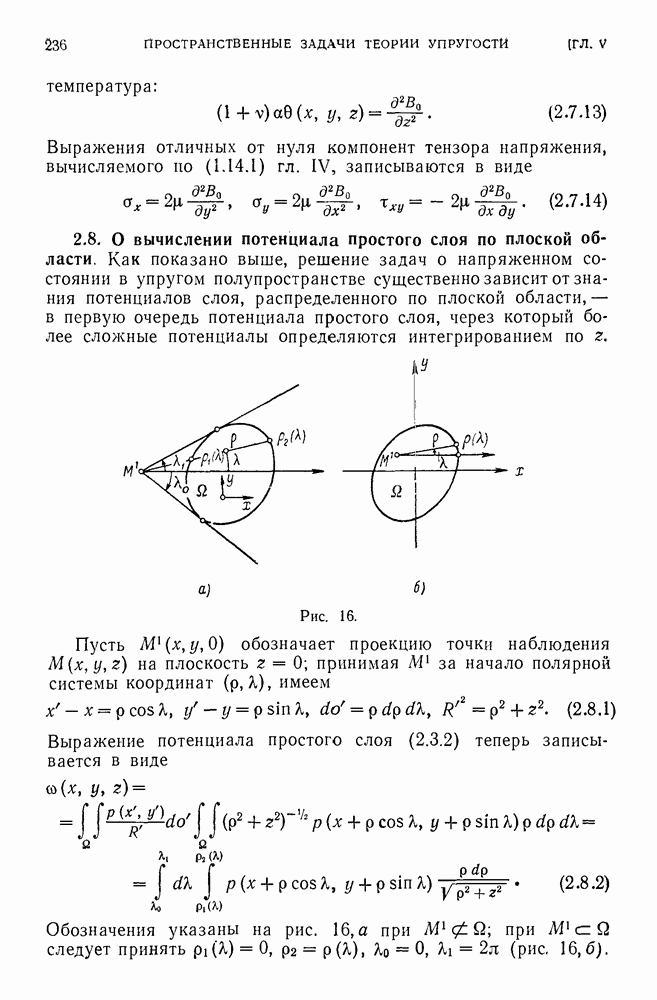
- 2.8. О вычислении потенциала простого слоя по плоской области.
- 2.9. Задача Дирихле для полупространства.
- 2.10. Первая краевая задача для полупространства.
- 2.11. Смешанные задачи для полупространства.
- 2.12. О принципе Сен-Венана. Формулировка Мизеса.
- 2.13. Сверхстатическая система сил.
- 2.14. Теоремы Стернберга (1954).
- § 3. Равновесие упругой сферы
- 3.2. Первая краевая задача.
- 3.3. Эластостатическая задача Робена для шара.
- 3.4. Тепловые напряжения в шаре.
- 3.5. Вторая краевая задача для сферы.
- 3.6. Вычисление вектора перемещения.
- 3.7. Напряженное состояние в центре шара.
- 3.9. Напряженное состояние в окрестности сферической полости.
- 3.10. Напряженное состояние в окрестности малой сферической полости в скрученном цилиндрическом стержне.
- 3.11. Действие массовых сил.
- 3.12. Гравитирующий шар.
- 3.13. Вращающийся шар.
- 3.14. Действие сосредоточенных сил.
- 3.15. Случай распределенной нагрузки.
- § 4. Тела вращения
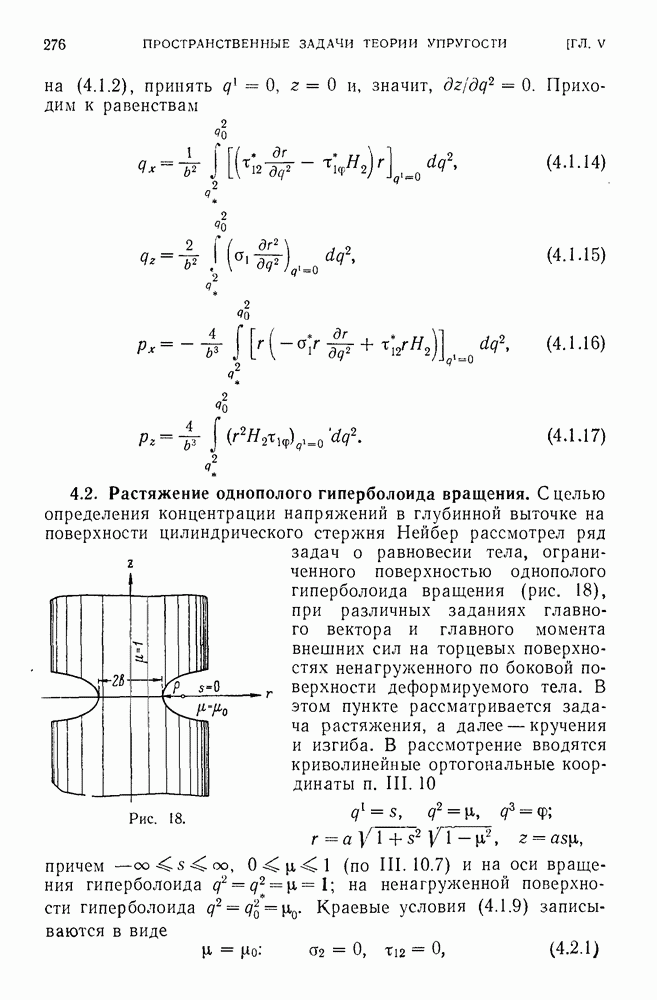
- 4.2. Растяжение однополого гиперболоида вращения.
- 4.3. Кручение гиперболоида.
- 4.4. Изгиб гиперболоида.
- 4.5. Вращающийся эллипсоид вращения.
- § 5. Эллипсоид
- 5.1. Эластостатическая задача Робена для трехосного эллипсоида.
- 5.3. Распределение напряжений по поверхности эллипсоида.
- 5.4. Перемещение поворота.
- 5.5. Распределение напряжений по поверхности эллипсоида.
- 5.6. Эллипсоидальная полость в неограниченной упругой среде.
- 5.7. Краевые условия.
- 5.8. Выражения постоянных через три параметра.
- 5.9. Сфероидальная полость в упругой среде.
- 5.10. Круговая щель в упругой среде.
- 5.11. Эллиптическая щель в упругой среде.
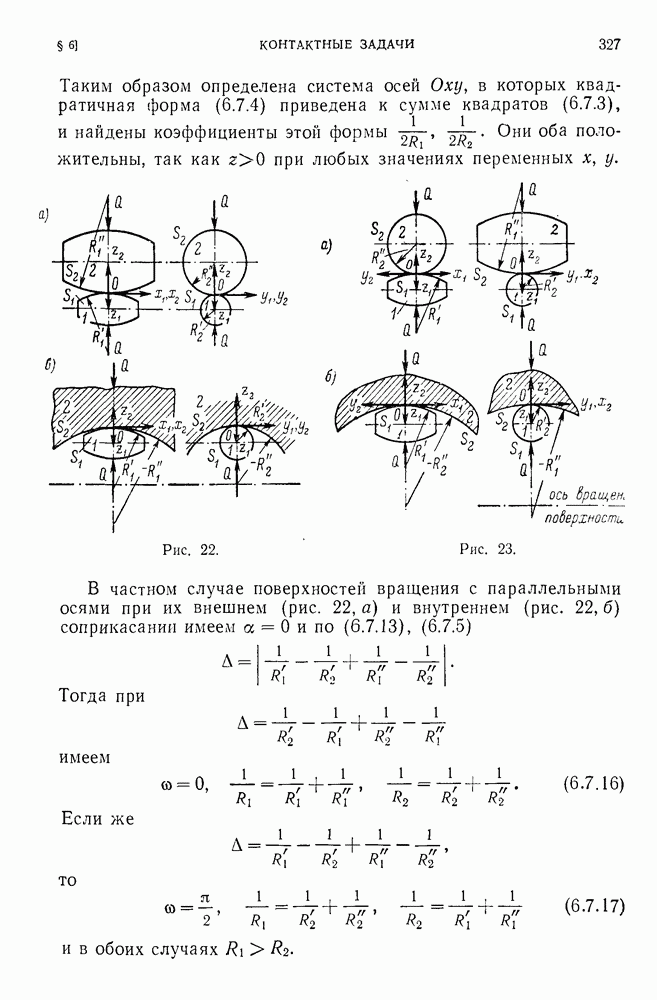
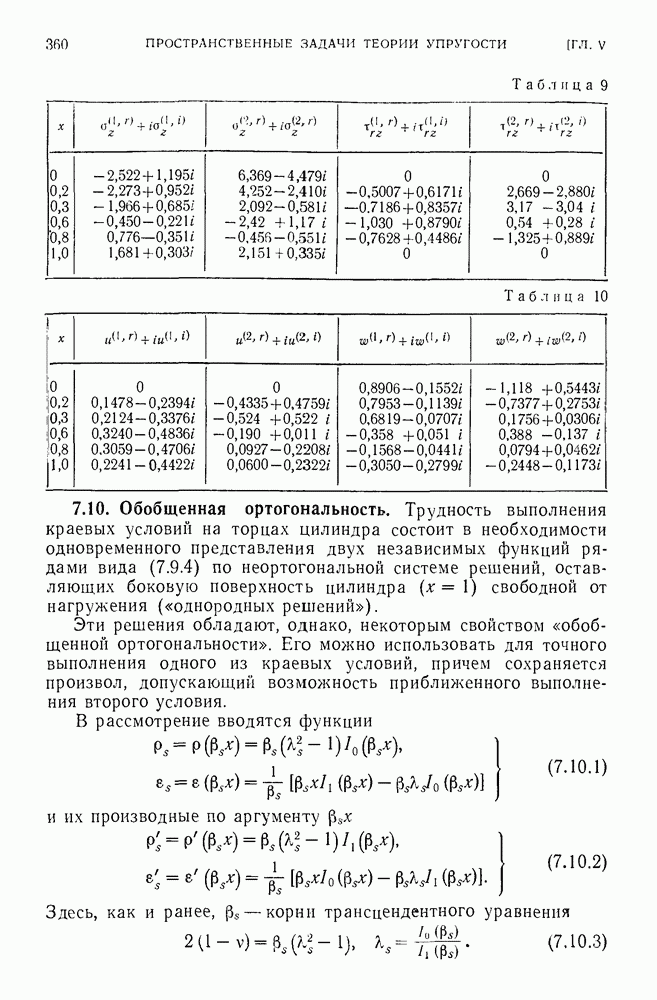
- § 6. Контактные задачи
- 6.1. Задача о жестком штампе. Краевое условие.
- 6.2. Способ решения задачи о жестком штампе.
- 6.2а. Представление сил и моментов, прилагаемых к неплоскому штампу.
- 6.3. Плоский, эллиптический в плане штамп.
- 6.4. Перемещения и напряжения.
- 6.5. Неплоский штамп.
- 6.5а. Определение сил и моментов, действующих на неплоский, эллиптический в плане штамп.
- 6.6. Перемещения и напряжения.
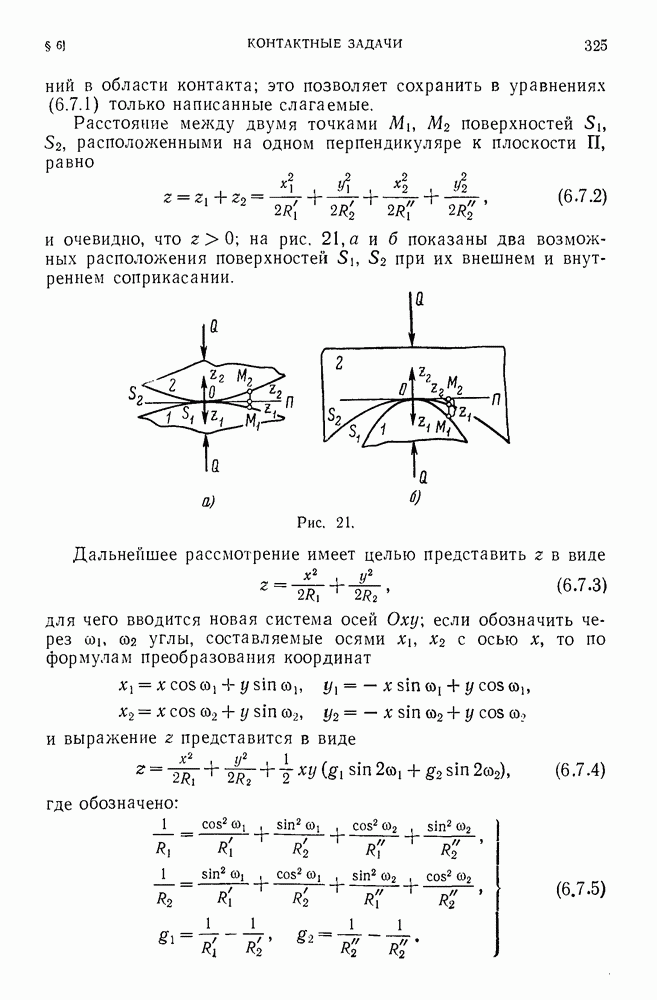
- 6.7. Соприкасание поверхностей.
- 6.8. Задача Герца о сжатии упругих тел.
- § 7. Равновесие упругого кругового цилиндра
- 7.2. Задача Ляме для полого цилиндра.
- 7.3. Дисторсии в полом цилиндре.
- 7.4. Полиномиальные решения задачи о равновесии цилиндра.
- 7.5. Кручение полого цилиндра силами, распределенными по торцу.
- 7.6. Решения в бесселевых функциях.
- 7.7. Задача Файлона.
- 7.8. Однородные решения.
- 7.9. Краевые условия на торцах.
- 7.10. Обобщенная ортогональность.
- ГЛАВА VI. ЗАДАЧА СЕН-ВЕНАНА
- 1.1. Постановка задачи Сен-Венана.
- 1.2. Интегральные уравнения равновесия.
- 1.3. Основные предположения.
- 1.4. Нормальное напряжение в задаче Сен-Венана.
- 1.5. Касательные напряжения
- § 2. Приведение к краевым задачам для уравнений Лапласа и Пуассона
- 2.2. Перемещения в задаче Сен-Венана.
- 2.3. Упругая линия.
- 2.4. Классификация задач Сен-Венана.
- 2.5. Определение постоянной а.
- 2.6. Центр жесткости.
- 2.7. Элементарные решения.
- § 3. Задача о кручении
- 3.2. Перемещения.
- 3.3. Теорема о циркуляции касательных напряжений.
- 3.4. Жесткость при кручении.
- 3.5. Мембранная аналогия Прандтля (1904).
- 3.6. Кручение стержня эллиптического сечения.
- 3.7. Неравенства для жесткости при кручении.
- 3.8. Кручение стержня прямоугольного сечения.
- 3.9. Решения в конечном виде.
- 3.10. Двусвязная область.
- 3.11. Эллиптическое кольцо.
- 3.12. Эксцентрическое кольцо.
- 3.13. Вариационное определение функции напряжений.
- 3.14. Приближенное решение задачи кручения.
- 3.15. Удлиненные профили.
- 3.16. Кручение тонкостенной трубы.
- 3.17. Многосвязные области.
- § 4. Изгиб силой
- 4.2. Изгиб стержня эллиптического поперечного сечения.
- 4.3. Функция напряжений С. П. Тимошенко.
- 4.4. Прямоугольное поперечное сечение.
- 4.5. Вариационная формулировка задачи изгиба.
- 4.6. Центр жесткости.
- 4.7. Приближенные решения.
- 4.8. Авиационный профиль.
- § 5. Задача Мичелла
- 5.2. Распределение нормальных напряжений.
- 5.3. Растяжение стержня.
- 5.3а. Растяжение стержня силами постоянной интенсивности.
- 5.4. Касательные напряжения
- 5.5. Напряжения
- 5.6. Определение …
- 5.7. Изгиб тяжелого стержня.
- 5.8. Средние значения напряжений.
- 5.9. О задаче Альманзи.
- ГЛАВА VII. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
- 1.2. Функция напряжений Эри.
- 1.3. Дифференциальное уравнение для функции напряжений.
- 1.4. Плоское напряженное состояние.
- 1.5. Обобщенное плоское напряженное состояние.
- 1.6. Плоская задача.
- 1.7. Перемещения в плоской задаче.
- 1.8. Главный вектор и главный момент.
- 1.9. Ортогональные криволинейные координаты.
- 1.10. Полярные координаты на плоскости.
- 1.11. Представление бигармонической функции.
- 1.12. Введение комплексного переменного.
- 1.13. Преобразование формул плоской задачи.
- 1.14. Формула Гурса.
- 1.15. Перенос начала координат.
- § 2. Балка и брус с круговой осью
- 2.2. Плоская задача Сен-Венана.
- 2.3. Операторное представление решений.
- 2.4. Функция напряжений в задаче о полосе.
- 2.5. Элементарная теория балки.
- 2.6. Полиномиальное нагружение (Менаже, 1901).
- 2.7. Синусоидальное нагружение (решения Рибьера (1898) и Файлона (1903)).
- 2.8. Сосредоточенная сила (Карман и Зеевальд, 1927).
- 2.9. Брус с круговой осью, нагруженный по торцам (Головин, 1881).
- 2.10. Нагружение кругового бруса по поверхности.
- 2.11. Косинусоидальное нагружение.
- 2.12. Однородные решения.
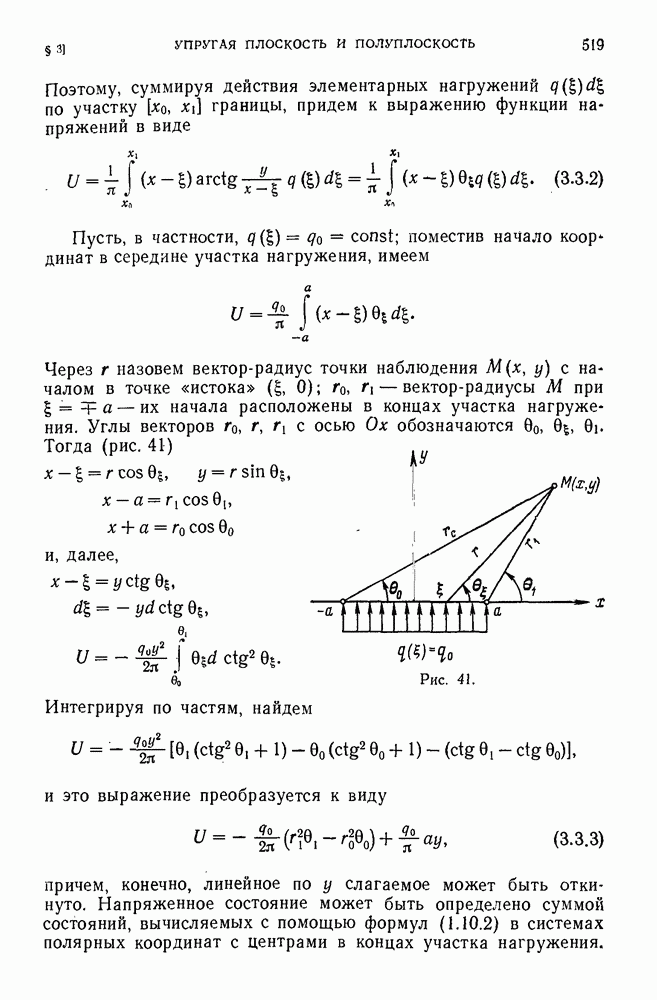
- § 3. Упругая плоскость и полуплоскость
- 3.1. Сосредоточенная сила и сосредоточенный момент в упругой плоскости.
- 3.2. Задача Фламана (1892).
- 3.3. Общий случай нормального нагружения.
- 3.4. Нагружение силой, направленной вдоль границы.
- 3.5. Плоская контактная задача.
- 3.6. Построение потенциала w.
- 3.7. Плоский штамп.
- 3.8. Штамп параболического очертания.
- 3.9. Сосредоточенная сила в упругой полуплоскости.
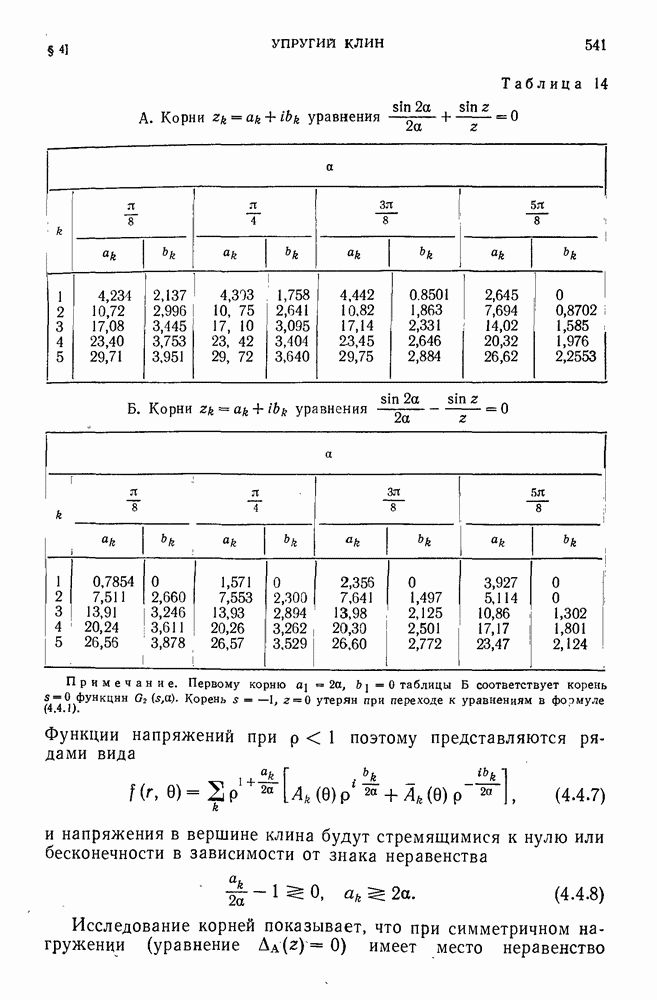
- § 4. Упругий клин
- 4.1. Сосредоточенная сила в вершине клина.
- 4.2. Интегральное преобразование Меллина в задаче о клине.
- 4.3. Сосредоточенный момент в вершине клина.
- 4.4. Нагружение боковых граней.
- § 5. Краевые задачи плоской теории упругости
- 5.2. Краевые задачи для односвязной конечной области.
- 5.3. Степень определенности функций Н. И. Мусхелишвили.
- 5.4. Бесконечная область с отверстием.
- 5.5. Двусвязная область. Дисторсия.
- 5.6. Представление функции напряжений в двусвязной области (Мичелл).
- 5.7. Тепловые напряжения. Плоская деформация.
- 5.8. Плоское напряженное состояние.
- 5.9. Стационарное распределение температуры.
- 5.10. Теорема Коши, интеграл Коши.
- 5.11. Интегралы типа Коши. Формулы Сохоцкого — Племели.
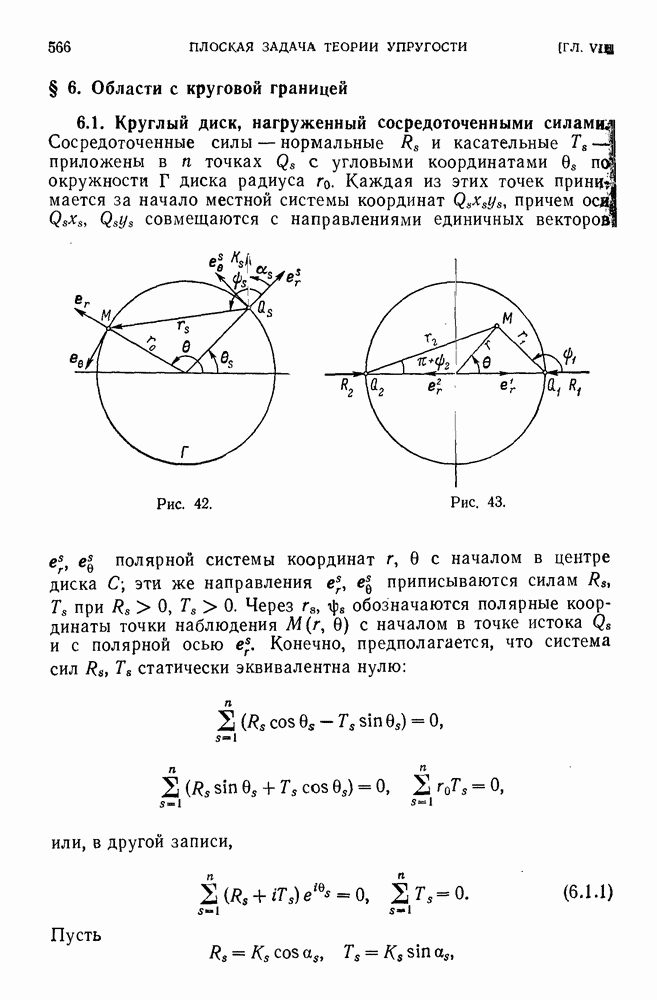
- § 6. Области с круговой границей
- 6.2. Общий случай нагружения круглого диска.
- 6.3. Способ интегралов Коши.
- 6.4. Нормальное напряжение на окружности.
- 6.5. Напряжения в центре диска.
- 6.6. Статически неуравновешенный вращающийся диск.
- 6.7. Первая краевая задача для круга.
- 6.8. Напряженное состояние.
- 6.9. Тепловые напряжения в диске, заключенном в жесткую обойму.
- 6.10. Круговое отверстие в бесконечной плоскости.
- 6.11. Равномерное нагружение края отверстия.
- 6.12. Растяжение плоскости, ослабленной круговым отверстием.
- 6.13. Продолжение Ф(z)
- 6.14. Решение краевых задач пп. 6.2, 6.10 способом продолжения.
- § 7. Круговое кольцо
- 7.2. Вторая краевая задача для кругового кольца.
- 7.3. Определение функций …
- 7.4. Труба под равномерным внешним и внутренним давлением (задача Ляме).
- 7.5. Температурные напряжения в кольце.
- 7.6. Растяжение кольца сосредоточенными силами.
- 7.7. Способ продолжения.
- § 8. Применение конформного преобразования
- 8.2. Способ интегралов Коши.
- 8.3. Эллиптическое отверстие.
- 8.4. Гипотрохоидное отверстие.
- 8.5. Односвязная конечная область.
- 8.6. Пример.
- 8.7. Первая краевая задача.
- 8.8. Эллиптическое отверстие.
- 8.9. Двусвязная область.
- 8.10. Неконцентрическое кольцо.
- ЧАСТЬ IV. ОСНОВНЫЕ СООТНОШЕНИЯ НЕЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ
- 1.1. Идеально-упругое тело.
- 1.2. Потенциалы деформации.
- 1.3. Однородное изотропное идеально-упругое тело.
- § 2. Закон состояния изотропного идеально-упругого тела
- 2.2. Начальное и натуральное состояния.
- 2.3. Связь между обобщенными модулями при различных начальных состояниях.
- 2.4. Представление тензора напряжений.
- 2.5. Выражение закона состояния через тензоры деформации.
- 2.6. Главные напряжения.
- 2.7. Выражение тензора напряжений.
- 2.8. Тензор напряжений Пиола (1836) — Кирхгоффа (1850).
- 2.9. О задании удельной потенциальной энергии деформации.
- § 3. Представление закона состояния квадратичным трехчленом
- 3.2. Представление энергетического тензора напряжений.
- 3.3. Представление тензора напряжений.
- 3.4. Разбиение тензора напряжений на шаровой тензор и девиатор.
- 3.5. Применение логарифмической меры деформации.
- § 4. Аппроксимации законов состояния
- 4.2. Зависимость коэффициентов квадратичного закона от начального состояния.
- 4.3. Знак удельной потенциальной энергии деформации.
- 4.4. Применение к задачам об одноосном растяжении.
- 4.5. Простой сдвиг.
- 4.6. Закон состояния Мурнагана.
- 4.7. Поведение материала при сверхвысоких давлениях.
- 4.8. Одноосное растяжение.
- 4.9. Несжимаемый материал.
- 4.10. Материалы с углом подобия девиаторов, равным нулю.
- § 5. Вариационные теоремы статики нелинейно-упругого тела
- 5.2. Стационарность потенциальной энергии системы.
- 5.3. Дополнительная работа деформации.
- 5.4. Стационарность дополнительной работы.
- 5.5. Удельная дополнительная работа деформации для полулинейного материала.
- ГЛАВА IX. ЗАДАЧИ И МЕТОДЫ НЕЛИНЕЙНОЙ ТЕОРИИ УПРУГОСТИ
- 1.1. Тензор напряжений при аффинном преобразовании.
- 1.2. Всестороннее сжатие.
- 1.3. Одноосное растяжение.
- 1.4. Простой сдвиг.
- § 2. Упругий слой
- 2.2. Сжатие и растяжение упругой полосы.
- 2.3. Уравнения статики.
- 2.4. Сжатие слоя.
- 2.5. Растяжение слоя.
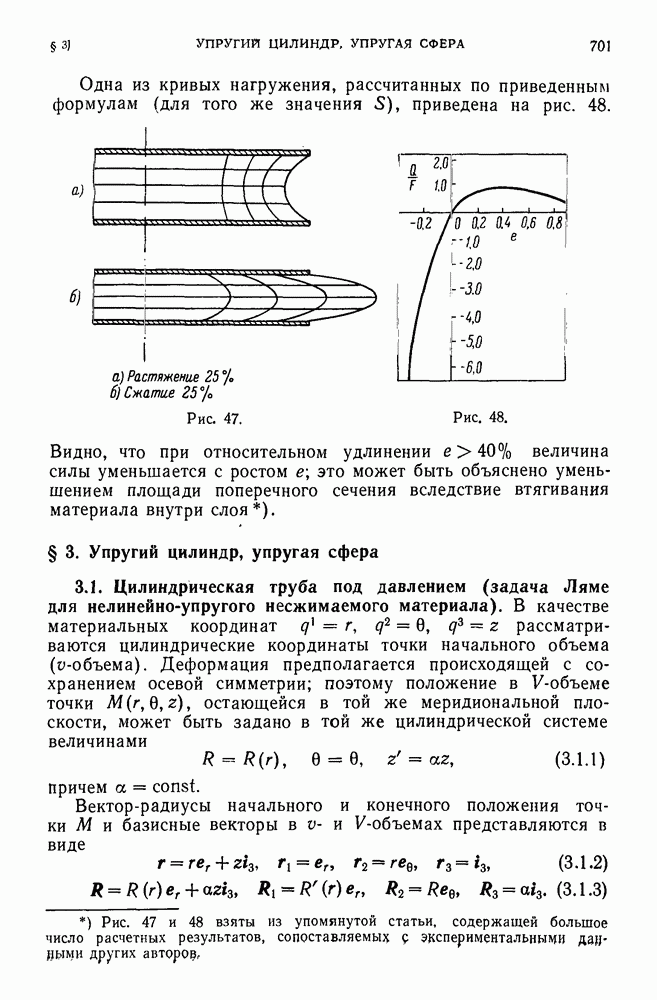
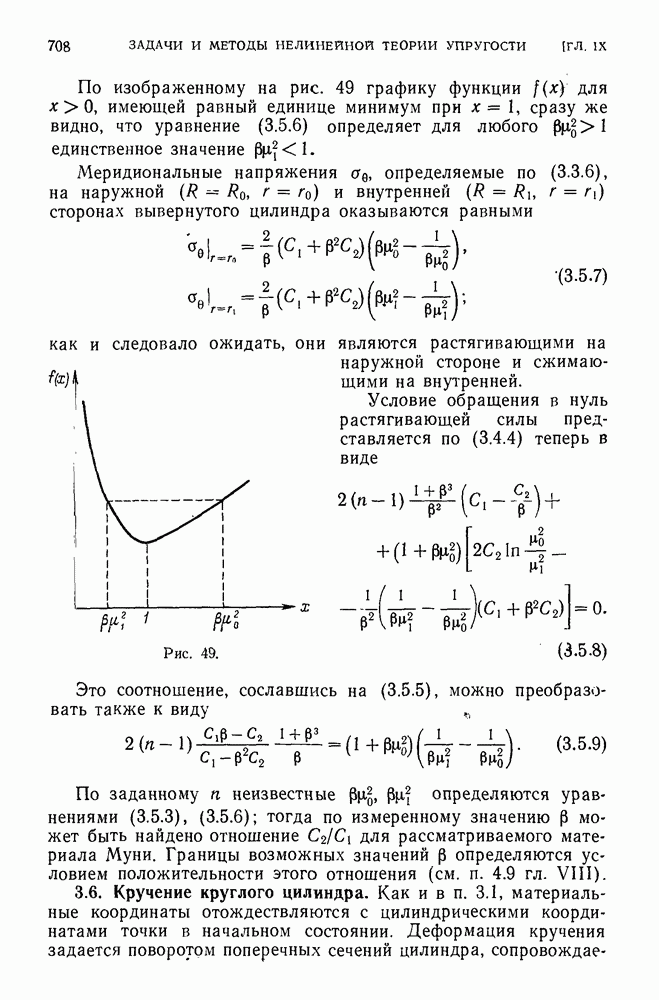
- § 3. Упругий цилиндр, упругая сфера
- 3.2. Напряжения.
- 3.3. Определение постоянных.
- 3.4. Материал Муни.
- 3.5. Цилиндр, «вывернутый наизнанку».
- 3.6. Кручение круглого цилиндра.
- 3.7. Напряжения, крутящий момент, осевая сила.
- 3.8. Симметричная деформация полого шара (задача Ляме для шара).
- 3.9. Несжимаемый материал.
- 3.10. Применение принципа стационарности потенциальной энергии.
- § 4. Малая деформация при наличии начального нагружения
- 4.2. Тензор напряжений.
- 4.3. Необходимые условия равновесия.
- 4.4. Представление тензора «тета».
- 4.5. Трехосное напряженное состояние.
- 4.6. Гидростатическое напряженное состояние.
- 4.7. Одноосное растяжение.
- 4.8. Деформация кручения сжатого стержня.
- § 5. Эффекты второго порядка
- 5.2. Уравнения равновесия.
- 5.3. Эффекты второго порядка.
- 5.3а. Изменение объема тела, подвергнутого дисторсии.
- 5.4. Выбор исходного приближения.
- 5.5. Эффекты второго порядка в задаче о кручении стержня.
- 5.6. Несжимаемая среда.
- 5.7. Уравнения равновесия.
- § 6. Плоская задача
- § 7. Полулинейный материал
- 7.2. Сохранение главных направлений.
- 7.3. Примеры (цилиндр и сфера).
- 7.4. Плоская деформация.
- 7.5. Напряженное состояние при плоском аффинном преобразовании.
- 7.6. Изгибание полосы в цилиндрическую панель.
- 7.7. Наложение малой деформации.
- 7.8. Случай сохранения главных направлений.
- 7.9. Уравнения нейтрального равновесия Саусвелла (1913).
- 7.10. Представление решений уравнений Саусвелла.
- 7.11. Бифуркация равновесия сжатого стержня.
- 7.12. Стержень круглого поперечного сечения.
- 7.13. Бифуркация равновесия полой сферы, сжатой равномерно распределенным давлением.
- ПРИЛОЖЕНИЕ I. ОСНОВЫ ТЕНЗОРНОЙ АЛГЕБРЫ
- 1.2. Символы Леви-Чивита.
- 1.3. Тензор второго ранга.
- 1.4. Простейшие операции с тензорами.
- 1.5. Диада векторов, диадное представление тензора второго ранга.
- 1.6. Тензоры высших рангов. Свертывание индексов.
- 1.7. Обратный тензор.
- 1.8. Тензор поворота.
- 1.9. Главные оси и главные значения симметричного тензора.
- 1.10. Выражение компонент тензора через главные значения. Инварианты. Теорема Кейли-Гамильтона.
- 1.10а. Главные оси и главные значения несимметричного тензора.
- 1.11. Разбиение симметричного тензора второго ранга на девиатор и шаровой тензор.
- 1.12. Функции тензоров.
- 1.13. Выделение шаровой и девиаторной частей.
- 1.14. Линейная связь между тензорами.
- ПРИЛОЖЕНИЕ II. ОСНОВНЫЕ ОПЕРАЦИИ ТЕНЗОРНОГО АНАЛИЗА
- II.2. Дифференциальные операции в векторном поле.
- II.3. Дифференциальные операции над тензорами.
- II.4. Двукратное дифференцирование.
- II.5. Преобразование объемного интеграла в поверхностный.
- II.6. Преобразование Стокса.
- ПРИЛОЖЕНИЕ III. ОРТОГОНАЛЬНЫЕ КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
- III.2. Квадрат линейного элемента.
- III.3. Ортогональная криволинейная система координат. Базисные векторы.
- III.4, Дифференцирование базисных векторов.
- III.5. Дифференциальные операции в ортогональных криволинейных координатах.
- III.6. Зависимости Ляме.
- III.7. Цилиндрические координаты.
- III.8. Сферические координаты.
- III.9. Тела вращения.
- III.10. Вырожденные эллиптические координаты.
- III.11. Эллиптические координаты (общий случай).
- ПРИЛОЖЕНИЕ IV. ТЕНЗОРНАЯ АЛГЕБРА В КОСОУГОЛЬНОМ БАЗИСЕ
- IV.2. Вектор в косоугольном базисе.
- IV.3. Метрический тензор.
- IV.4. Тензор Леви-Чивита.
- IV.5. Тензоры в косоугольном базисе.
- IV.6. Преобразование базиса.
- IV.7. Главные оси симметричного тензора. Главные инварианты.
- ПРИЛОЖЕНИЕ V. ОПЕРАЦИИ ТЕНЗОРНОГО АНАЛИЗА В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- V.2. Производные базисных векторов.
- V.3. Ковариантное дифференцирование.
- V.4. Дифференциальные операции в криволинейных координатах.
- V.5. Переход к ортогональным криволинейным координатам.
- V.6. Тензор Римана — Кристоффеля.
- V.7. Тензор …
- V.8. Преобразование поверхностного интеграла в объемный.
- ПРИЛОЖЕНИЕ VI. СВЕДЕНИЯ ПО ТЕОРИИ СФЕРИЧЕСКИХ И ЭЛЛИПСОИДАЛЬНЫХ ФУНКЦИЙ
- VI.2. Сферические функции Лапласа.
- VI.3. Решения …
- VI.4. Решение внешней и внутренней задач для шара.
- VI.5. Внешняя и внутренняя задачи Дирихле для сжатого эллипсоида (сфероида).
- VI.6. Представление гармонических полиномов произведениями Ляме.
- VI.7. Функция …
- VI.8. Потенциалы простого слоя на эллипсоиде.
- ЛИТЕРАТУРНЫЕ УКАЗАНИЯ